题目内容
9.探究题:定义:对于实数a,符号[a]表示不大于a的最大整数.
例如:[5.7]=5,[-π]=-4.
(1)如果[a]=-2,那么a可以是A
A.-15 B.-2.5 C.-3.5 D.-4.5
(2)如果[$\frac{x+1}{2}$]=3,则整数x=5或6.
(3)如果[-1.6-$\frac{1}{6}$[$\frac{x+1}{2}$]]=-3,满足这个方程的整数x共有12个.
分析 (1)根据新定义解答即可得;
(2)由新定义得出3≤$\frac{x+1}{2}$<4,解之可得答案;
(3)令[$\frac{x+1}{2}$]=y,得[-1.6-$\frac{1}{6}$y]=-3,即-3≤-1.6-$\frac{1}{6}$y<-2,解之得出整数y的值,从而有[$\frac{x+1}{2}$]=3、4、5、6、7、8,再进一步求解可得.
解答 解:(1)根据题意知,[a]=-2表示不超过a的最大整数,
∴a可以是-15,
故选:A;
(2)根据题意得3≤$\frac{x+1}{2}$<4,
解得:5≤x<7,
则整数x=5或6,
故答案为:5或6;
(3)令[$\frac{x+1}{2}$]=y,
则原方程可变形为[-1.6-$\frac{1}{6}$y]=-3,
∴-3≤-1.6-$\frac{1}{6}$y<-2,
解得:2.4<y≤8.4,
则y可取的整数有3、4、5、6、7、8,
若y=3,则3≤$\frac{x+1}{2}$<4,解得:5≤x<7,其整数解有5、6;
若y=4,则4≤$\frac{x+1}{2}$<5,解得:7≤x<9,其整数解有7、8;
若y=5,则5≤$\frac{x+1}{2}$<6,解得:9≤x<11,其整数解有9、10;
若y=6,则6≤$\frac{x+1}{2}$<7,解得:11≤x<13,其整数解有11、12;
若y=7,则7≤$\frac{x+1}{2}$<8,解得:13≤x<15,其整数解有13、14;
若y=8,则8≤$\frac{x+1}{2}$<9,解得:15≤x<17,其整数解有15、16;
∴满足这个方程的整数x共有12个,
故答案为:12.
点评 本题主要考查解一元一次不等式组,理解新定义将方程转化为不等式组求解是解题的关键.

| A. | y=$\frac{3}{x}$ | B. | y=-x+5 | C. | y=$\frac{1}{2}$x | D. | y=$\frac{1}{2}{x^2}$(x<0) |
| A. | 小于 | B. | 等于 | C. | 大于 | D. | 都不是 |
| A. | 由5x=-4得x=-$\frac{5}{4}$ | B. | 由4x+2=3x-1得4x+3x=2-1 | ||
| C. | 由$\frac{x}{5}$-1=2得x-5=2 | D. | 由4x-3=2x-2得2x=1 |
| A. | m=3,n=1 | B. | m=5,n=1 | C. | m=3,n=-1 | D. | m=5,n=-1 |
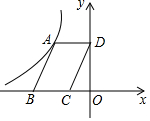 如图,点A是反比例函数y=$\frac{k}{x}$的图象上的一点,过A作?ABCD,使点B在x轴上,点D在y轴上,已知?ABCD的面积为6,则k的值为( )
如图,点A是反比例函数y=$\frac{k}{x}$的图象上的一点,过A作?ABCD,使点B在x轴上,点D在y轴上,已知?ABCD的面积为6,则k的值为( )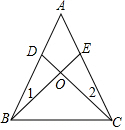 如图,在△ABC中,D,E分别是AB,AC边上的点,且∠1=∠2,CD=BE.CD与BE相交于点O.求证:
如图,在△ABC中,D,E分别是AB,AC边上的点,且∠1=∠2,CD=BE.CD与BE相交于点O.求证: