题目内容
19.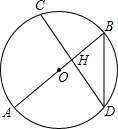 如图,AB是⊙O的直径,弦CD⊥AB于H,且CD=2$\sqrt{2}$,BD=$\sqrt{3}$,则AB的长为( )
如图,AB是⊙O的直径,弦CD⊥AB于H,且CD=2$\sqrt{2}$,BD=$\sqrt{3}$,则AB的长为( )| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
分析 连接OD,如图,先利用垂径定理得到CH=$\sqrt{2}$,再利用勾股定理计算出BH=1,设⊙O的半径为r,则OH=r-1,OD=r,利用勾股定理得到(r-1)2+($\sqrt{2}$)2=r2,解方程求出r即可得到直径AB的长.
解答 解:连接OD,如图,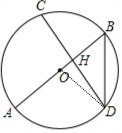
∵CD⊥AB,
∴DH=CH=$\frac{1}{2}$CD=$\sqrt{2}$,
在Rt△BDH中,BH=$\sqrt{(\sqrt{3})^{2}-(\sqrt{2})^{2}}$=1,
设⊙O的半径为r,则OH=r-1,OD=r,
在Rt△OHD中,(r-1)2+($\sqrt{2}$)2=r2,解得r=$\frac{3}{2}$,
∴AB=2r=3.
故选B.
点评 本题考查了圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.也考查了垂径定理.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
9.已知关于x的方程x2+2x-(m-2)=0有两个不相等的实数根,则m的取值范围是( )
| A. | m≥1 | B. | m≤1 | C. | m>1 | D. | m<1 |
10.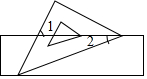 如图,把含有45°角的直角三角板的两个顶点放在直尺的对边上,如果∠1=65°,那么∠2的度数是( )
如图,把含有45°角的直角三角板的两个顶点放在直尺的对边上,如果∠1=65°,那么∠2的度数是( )
 如图,把含有45°角的直角三角板的两个顶点放在直尺的对边上,如果∠1=65°,那么∠2的度数是( )
如图,把含有45°角的直角三角板的两个顶点放在直尺的对边上,如果∠1=65°,那么∠2的度数是( )| A. | 15° | B. | 20° | C. | 25° | D. | 30° |
14. 如图,AB∥CD,BC平分∠ABF,若∠BFC=44°,则∠BCF的度数为( )
如图,AB∥CD,BC平分∠ABF,若∠BFC=44°,则∠BCF的度数为( )
 如图,AB∥CD,BC平分∠ABF,若∠BFC=44°,则∠BCF的度数为( )
如图,AB∥CD,BC平分∠ABF,若∠BFC=44°,则∠BCF的度数为( )| A. | 56° | B. | 60° | C. | 68° | D. | 74° |
4.七(1)班人数的40%是女生,七(2)班人数的45%是女生,两班女生人数相等,那么七(1)班的人数( )七(2)班的人数.
| A. | 小于 | B. | 等于 | C. | 大于 | D. | 都不是 |
2.下列各式计算正确的是( )
| A. | $\sqrt{5}$+$\sqrt{2}$=$\sqrt{7}$ | B. | 5$\sqrt{6}$-3$\sqrt{3}$=2$\sqrt{3}$ | C. | ($\sqrt{8}$+$\sqrt{50}$)÷2=$\sqrt{4}$+$\sqrt{25}$=7 | D. | 3$\sqrt{3}$+$\sqrt{27}$=6$\sqrt{3}$ |
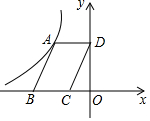 如图,点A是反比例函数y=$\frac{k}{x}$的图象上的一点,过A作?ABCD,使点B在x轴上,点D在y轴上,已知?ABCD的面积为6,则k的值为( )
如图,点A是反比例函数y=$\frac{k}{x}$的图象上的一点,过A作?ABCD,使点B在x轴上,点D在y轴上,已知?ABCD的面积为6,则k的值为( )