题目内容
下列事件中的不可能事件是( )
A. 通常加热到100 ℃时,水沸腾
B. 抛掷2枚正方体骰子,都是6点朝上
C. 经过有交通信号灯的路口,遇到红灯
D. 任意画一个三角形,其内角和是360°
D
【解析】A. 是必然事件，选项错误；
B. 是随机事件，选项错误；
C. 是随机事件，选项错误；
D. 是不可能事件，选项正确。
故选：D.
练习册系列答案
相关题目
桌面上有A、B两球，若要将B球射向桌面任意一边，使一次反弹后击中A，则如图所示8个点中，可以瞄准的点的个数（ ）
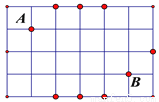
A. 1 B. 2 C. 4 D. 6
B
【解析】利用轴对称的性质准确画出图形即可得出答案.
【解析】
要想一次反弹后击中A，需要入射角也反射角相等，因此，可以经过如下图所示的两条路径达到要求，即B-D-A或者B-C-A，另外的一次反弹路线，都不经过图中给出的点，故选B. 如图，在梯形ABCD中，CD∥AB，且CD=6cm，AB=9cm，P、Q分别从A、C同时出发，P以1cm/s的速度由A向B运动，Q以2cm/s的速度由C向D运动．则________秒时，直线QP将四边形ABCD截出一个平行四边形
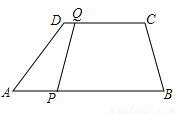
2或3
【解析】【解析】
设x秒时，直线QP将四边形ABCD截出一个平行四边形，则AP=xcm，BP=（9-x）cm，CQ=2xcm，DQ=（6-2x）cm．
∵CD∥AB，∴分两种情况：
1．当AP=DQ时，x=6-2x，解得：x=2；
2．当BP=CQ时，9-x=2x，解得：x=3；
综上所述：当2秒或3秒时，直线QP将四边形ABCD截出一个平行四边形．
... 小明每天早上要在7:50之前赶到距家1 000 m的学校上学.一天早上,小明以80 m/min的速度出发去上学.5 min后,小明的爸爸发现小明忘了带数学书,于是,爸爸立即以100 m/min的速度去追赶小明,结果在途中追上了小明.试探究这个事件是什么事件.
不可能事件
【解析】试题分析：根据题目所给题设条件可知，这是考查一元一次方程的应用问题，关键在于弄清题意，找出等量关系即：小明爸爸和小明所行路程相等，列出方程求解．
解:是不可能事件.理由如下:
设小明的爸爸用x min追上小明,则可列方程
80(x+5)=100x,解得x=20.此时80(x+5)=80×(20+5)=2 000>1 000,说明这时小明已经到学校了,故小... 下列说法正确的是( )
A. 可能性很小的事件在一次试验中一定不会发生
B. 可能性很小的事件在一次试验中一定发生
C. 可能性很小的事件在一次试验中有可能发生
D. 不可能事件在一次试验中也可能发生
C
【解析】试题分析：在随机试验中，可能出现也可能不出现，而在大量重复试验中具有某种规律性的事件叫做随机事件；不可能事件是指在大量重复实验中完全不会发生的事件. 计算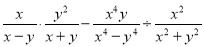
【解析】试题分析：分式乘除法和减法的混合运算应根据运算顺序先算乘除后算加减.
试题解析：
原式= 化简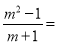
__________
【解析】试题解析：
故答案为： 计算
【解析】试题分析：分母相同，按照同分母分式加减的法则进行计算，分子合并同类项后再进行约分化简．
试题解析：
【解析】
原式＝
＝
＝． 求出不等式3x－2≥4(x－1)的所有非负整数解．
不等式的解集是x≤2，故不等式3x－2≥4(x－1)的非负整数解为0,1,2.
【解析】【试题分析】去括号得： 移项得： 合并得： ，系数化为1得：x≤2，所以不等式的非负整数解为0,1,2.
【试题解析】
去括号得：
移项得：
合并得： ，
系数化为1得：x≤2，
所以不等式的非负整数解为0,1,2.