题目内容
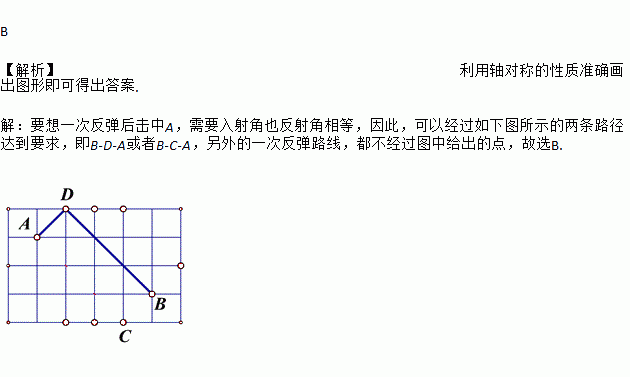
桌面上有A、B两球，若要将B球射向桌面任意一边，使一次反弹后击中A，则如图所示8个点中，可以瞄准的点的个数（ ）
A. 1 B. 2 C. 4 D. 6
B
【解析】利用轴对称的性质准确画出图形即可得出答案.
【解析】
要想一次反弹后击中A，需要入射角也反射角相等，因此，可以经过如下图所示的两条路径达到要求，即B-D-A或者B-C-A，另外的一次反弹路线，都不经过图中给出的点，故选B.
练习册系列答案
夺冠训练单元期末冲刺100分系列答案
新思维小冠军100分作业本系列答案
名师指导一卷通系列答案
相关题目
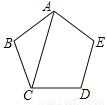
如图，AC是正五边形ABCDE的一条对角线，则∠ACB= ．
36°．
【解析】
试题分析：∵五边形ABCDE是正五边形，∴∠B=108°，AB=CB，∴∠ACB=（180°﹣108°）÷2=36°；故答案为：36°． 有如图所示的两种广告牌，其中图（1）是由两个等腰直角三角形构成的，图（2）是一个矩形，从图形上确定这两个广告牌面积的大小关系，并将这种大小关系用含字母a，b的不等式表示为__________．
a2＋b2＞ab (a≠b)
【解析】试题分析：由图上可看出：图1可看做是长为a，宽为b的长方形加上一个小直角三角形；图2可看做是长为a，宽为b的长方形，根据不等关系：图1的面积＞图2的面积，即可列出不等式．
根据图形的面积公式，得图1的面积是a2＋b2，图2的面积是ab
再根据图形的面积大小关系，得a2＋b2＞ab（a≠b）. 如图△ABC中，AB=BC，∠A=36°，BD平分∠ABC交AC于D，则图中的等腰三角形有_____个
3
【解析】根据条件求出各个角的度数，由此确定哪个三角形是等腰三角形
解答：∵在△ABC中，AB=BC，∠A=36°，
∴∠ABC=∠ACB =72°，
∵BD平分∠ABC，
∴∠ABD=∠CBD =36°，
∴∠ABD=∠A =36°，∠BDC =72°=∠C，
∴△ABD和△BDC都是等腰三角形.
故有三个等腰三角形 故有三个. 如图，△ABC与△A′B′C′关于直线MN对称，P为MN上任一点，下列结论中错误的是（ ）
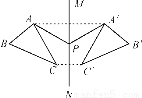
A. △AA′P是等腰三角形 B. MN垂直平分AA′，CC′
C. △ABC与△A′B′C′面积相等 D. 直线AB、A′B′的交点不一定在MN上
D
【解析】试题分析：△ABC与△A′B′C′关于直线MN对称，P为MN上任一点，所以根据轴对称图形的性质可以知道图形上对应点的连线被对称轴垂直且平分，所以△AA′P是等腰三角形；MN垂直平分AA′，CC′；△ABC与△A′B′C′面积相等；AA′已知∠AOB＝30°，点P在∠AOB的内部，点P1和点P关于OA对称，点P2和点P关于OB对称，则P1、O、P2三点构成的三角形是（ ）
A. 直角三角形 B. 钝角三角形 C. 等腰直角三角形 D. 等边三角形
D
【解析】
连接OP，
∵点P1和点P关于OA对称，点P2和点P关于OB对称，
∴OA垂直平分PP1，OB垂直平分PP2，
∴OP=OP1，OP=OP2，
∴OP1=OP2，∠P1OA=∠AOP，∠P2OB=∠BOP，
∵∠AOB=30°，
∴∠P1O P2=∠P1O P+∠P2O P=2∠AOP+2∠BOP=2（∠AOP+∠BOP）=2∠AOB=... 找出图中是轴对称图形的图形,并找出两对对应点、两对对应线段、两对对应角.
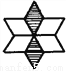
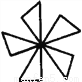
（1） (2) (3)
见解析
【解析】试题分析：本题考查了利用轴对称设计图案的知识,解答本题的关键是熟练掌握轴对称的性质.观察可知①是轴对称图形,先确定对称轴,然后找对应点、对应线段及对应角.
【解析】
第一个图形是轴对称图形，第二、三个图形是旋转对称图形.
如上图所示，若以EF为对称轴,则点A与点B、点M与点N、点C与点D等是对应点.线段AG与BH、CM与DN、PG与PH等是对应线段,∠A与∠B、... 观察下列平面图形：其中属于轴对称图形的有( )
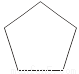
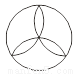
A. 1个 B. 2个 C. 3个 D. 4个
C
【解析】根据轴对称图形的定义可知，前三个图形分别有5条、5条、3条对称轴，最后一个图形三角形内的图案没有对称轴.
故选C. 下列事件中的不可能事件是( )
A. 通常加热到100 ℃时,水沸腾
B. 抛掷2枚正方体骰子,都是6点朝上
C. 经过有交通信号灯的路口,遇到红灯
D. 任意画一个三角形,其内角和是360°
D
【解析】A. 是必然事件，选项错误；
B. 是随机事件，选项错误；
C. 是随机事件，选项错误；
D. 是不可能事件，选项正确。
故选：D.