题目内容
15.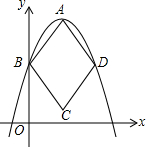 如图,在平面直角坐标系中,菱形ABCD的三个顶点A,B,D均在抛物线y=ax2-4ax+3(a<0)上.若点A是抛物线的顶点,点B是抛物线与y轴的交点,则点D的坐标为(4,3).
如图,在平面直角坐标系中,菱形ABCD的三个顶点A,B,D均在抛物线y=ax2-4ax+3(a<0)上.若点A是抛物线的顶点,点B是抛物线与y轴的交点,则点D的坐标为(4,3).
分析 需先求出点B的坐标和抛物线的对称轴,再根据点B与点D关于抛物线的对称轴对称即可求出点D的坐标.
解答 解:∵y=ax2-4ax+3的对称轴是x=-$\frac{-4a}{2a}$=2,与y轴的交点坐标是(0,3),
∴点B的坐标是(0,3),
∵菱形ABCD的三个顶点在二次函数y=ax2-4ax+3(a<0)的图象上,
点A、B分别是该抛物线的顶点和抛物线与y轴的交点,
∴点B与点D关于直线x=2对称,
∴点D的坐标为(4,3).
故答案为:(4,3).
点评 本题主要考查了二次函数的性质与菱形的性质,得出二次函数图象的对称轴是解题关键.

练习册系列答案
相关题目
20.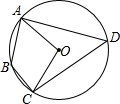 如图,四边形ABCD内接于⊙O,若∠B=130°,则∠AOC的大小是( )
如图,四边形ABCD内接于⊙O,若∠B=130°,则∠AOC的大小是( )
 如图,四边形ABCD内接于⊙O,若∠B=130°,则∠AOC的大小是( )
如图,四边形ABCD内接于⊙O,若∠B=130°,则∠AOC的大小是( )| A. | 130° | B. | 120° | C. | 110° | D. | 100° |
 如图,在△ABC中,BC=AC,将△ABC沿CD折叠(D在AB上),使得点A与点B恰好重合,如果AB=8cm,则BD=4cm.
如图,在△ABC中,BC=AC,将△ABC沿CD折叠(D在AB上),使得点A与点B恰好重合,如果AB=8cm,则BD=4cm.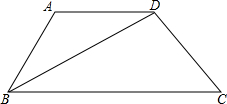 如图,AD∥BC,BD平分∠ABC,则图中的等腰三角形是△ABD.
如图,AD∥BC,BD平分∠ABC,则图中的等腰三角形是△ABD.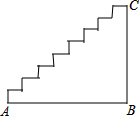 如图是小明家的楼梯示意图,其水平距离(即:AB的长度)为(2a+b)米,一只蚂蚁从A点沿着楼梯爬到C点,共爬了(3a-b)米.问小明家楼梯的竖直高点(即:BC的长度)为多少米.
如图是小明家的楼梯示意图,其水平距离(即:AB的长度)为(2a+b)米,一只蚂蚁从A点沿着楼梯爬到C点,共爬了(3a-b)米.问小明家楼梯的竖直高点(即:BC的长度)为多少米. 如图所示,网格中有△ABC和点D,请你找出另外两点E、F,在图中画出△DEF,使△ABC≌△DEF,且顶点A、B、C分别与D、E、F对应.
如图所示,网格中有△ABC和点D,请你找出另外两点E、F,在图中画出△DEF,使△ABC≌△DEF,且顶点A、B、C分别与D、E、F对应.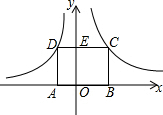 如图,矩形ABCD的顶点A在x轴负半轴上,点B在x轴正半轴,点C在反比例函数y=$\frac{4}{x}$第一象限的图象上,点D在反比例函数y=$\frac{k}{x}$的图象上,CD交y轴于点E.若DE:CE=1:2,则k的值是-2.
如图,矩形ABCD的顶点A在x轴负半轴上,点B在x轴正半轴,点C在反比例函数y=$\frac{4}{x}$第一象限的图象上,点D在反比例函数y=$\frac{k}{x}$的图象上,CD交y轴于点E.若DE:CE=1:2,则k的值是-2.