题目内容
14.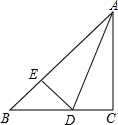 如图,在Rt△ABC中,∠C=90°,∠B=45°,AD平分∠BAC,交BC于点D,DE⊥AB于点E.
如图,在Rt△ABC中,∠C=90°,∠B=45°,AD平分∠BAC,交BC于点D,DE⊥AB于点E.(1)求证:AC=BD+DE;
(2)若AB=10cm,求△BDE的周长.
分析 (1)由角平分线的性质得出DE=DC,得出BD+DE=BC,再由AC=BC,即可得出结论;
(2)根据角平分线上的点到角的两边距离相等可得CD=DE,再利用“HL”证明Rt△ACD和Rt△AED全等,根据全等三角形对应边相等可得AC=AE,然后求出△DBE的周长=AB,即可得解.
解答 (1)证明:∵∠C=90°,
∴DC⊥AC,
∵AD平分∠BAC,DE⊥AB,
∴DE=DC,
∴BD+DE=BD+DC=BC,
又∵AC=BC,
∴BD+DE=AC.
(2)解:∵在Rt△ACD和Rt△AED中,
$\left\{\begin{array}{l}{AD=AD}\\{CD=DE}\end{array}\right.$,
∴Rt△ACD≌Rt△AED(HL),
∴AC=AE,
△DBE的周长=BD+DE+BE=BD+CD+BE=BC+BE=AC+BE=AE+BE=AB=10cm.
点评 本题考查了全等三角形的判定与性质,角平分线的性质、等腰直角三角形的性质;熟练掌握角平分线的性质,并能进行推理论证是解决问题的关键.

练习册系列答案
相关题目
4.如图,矩形纸片按图(1)中的虚线第一次折叠得图(2),折痕与矩形一边的形成的∠1=65°,再按图(2)中的虚线进行第二折叠得到图(3),则∠2的度数为( )
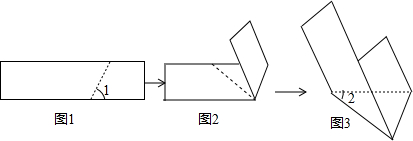

| A. | 20° | B. | 25° | C. | 30° | D. | 35° |
5.下列各组单项式中,不是同类项的是( )
| A. | 0.4x2y与0.3xy2 | B. | 2a2b与5ba2 | C. | 13与-$\frac{3}{2}$ | D. | -3x与7x |
2.如果分式$\frac{{x}^{2}-9}{3x+9}$的值为零,则x的值为( )
| A. | 9 | B. | 3 | C. | -3 | D. | ±3 |
6. 如图,利用标杆BE测量树CD的高度,如果标杆BE长为2米,测得AB=3米,AC=9米,且点A、E、D在一条直线上,则树CD是( )
如图,利用标杆BE测量树CD的高度,如果标杆BE长为2米,测得AB=3米,AC=9米,且点A、E、D在一条直线上,则树CD是( )
 如图,利用标杆BE测量树CD的高度,如果标杆BE长为2米,测得AB=3米,AC=9米,且点A、E、D在一条直线上,则树CD是( )
如图,利用标杆BE测量树CD的高度,如果标杆BE长为2米,测得AB=3米,AC=9米,且点A、E、D在一条直线上,则树CD是( )| A. | 6米 | B. | 7.5米 | C. | 8米 | D. | 8.5米 |
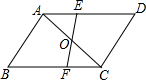 如图,在四边形ABCD中,AD∥BC,EF过AC的中点O,分别交AD,BC于点E,F.
如图,在四边形ABCD中,AD∥BC,EF过AC的中点O,分别交AD,BC于点E,F.