题目内容
14.已知一抛物线经过点A(-1,0),B(0,-5),且抛物线对称轴为直线x=2,求该抛物线的解析式.分析 因为对称轴是直线x=2,所以得到点(-1,0)的对称点是(5,0),因此利用交点式y=a(x-x1)(x-x2),求出解析式.
解答 解:∵抛物线对称轴是直线x=2且经过点(-1,0),
由抛物线的对称性可知:抛物线还经过点(5,0),
设抛物线的解析式为y=a(x-x1)(x-x2)(a≠0),
即:y=a(x+1)(x-5),
把B(0,-5)代入得:-5=-5a,
∴a=1.
∴抛物线的解析式为:y=x2-4x-5.
点评 本题考查了用待定系数法求函数解析式的方法,注意选择若知道与x轴的交点坐标,采用交点式比较简单.

练习册系列答案
相关题目
9.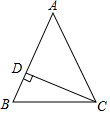 如图,等腰△ABC中,AB=AC,∠A=50°,CD⊥AB于D,则∠DCB等于( )
如图,等腰△ABC中,AB=AC,∠A=50°,CD⊥AB于D,则∠DCB等于( )
 如图,等腰△ABC中,AB=AC,∠A=50°,CD⊥AB于D,则∠DCB等于( )
如图,等腰△ABC中,AB=AC,∠A=50°,CD⊥AB于D,则∠DCB等于( )| A. | 30° | B. | 25° | C. | 15° | D. | 20° |
4.如果a是有理数,则下列各数中一定是正数的是( )
| A. | 2016a | B. | 2016+a | C. | |a| | D. | a2+0.0001 |
 如图,在△ACD和△ABD中,∠C=∠B=90°,要使△ACD≌△ABD,还需增加一个条件是CD=DB.
如图,在△ACD和△ABD中,∠C=∠B=90°,要使△ACD≌△ABD,还需增加一个条件是CD=DB.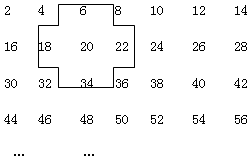 探索规律:将连续的偶数2,4,6,8,…,排成如表:
探索规律:将连续的偶数2,4,6,8,…,排成如表: