题目内容
7.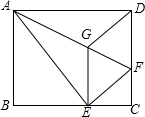 如图,将矩形ABCD沿AF折叠,使点D落在BC边的点E处,过点E作EG∥CD交AF于点G,连接DG.
如图,将矩形ABCD沿AF折叠,使点D落在BC边的点E处,过点E作EG∥CD交AF于点G,连接DG.(1)求证:四边形EFDG是菱形;
(2)若AG=7、GF=3,求DF的长.
分析 (1)连接DE交AF于H,先根据DF=EG,DF∥EG,判定四边形DFEG是平行四边形,再根据GF⊥DE,即可得出四边形EFDG是菱形;
(2)根据条件得到FH=$\frac{1}{2}$GF=$\frac{3}{2}$,AF=10,再根据Rt△ADF中,DH⊥AF,运用射影定理即可得到DF2=FH×FA,进而得出DF的长.
解答 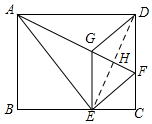 解:(1)如图,连接DE交AF于H,
解:(1)如图,连接DE交AF于H,
由折叠可得,AF⊥DE,DF=EF,∠DFG=∠EFG,
∵EG∥CD,
∴∠DFG=∠EGF,
∴∠EFG=∠EGF,
∴EG=EF,
∴DF=EG,
∵DF∥EG,
∴四边形DFEG是平行四边形,
∵GF⊥DE,
∴四边形EFDG是菱形;
(2)∵四边形EFDG是菱形,
∴FH=$\frac{1}{2}$GF=$\frac{3}{2}$,
∵AG=7,GF=3,
∴AF=10,
∵Rt△ADF中,DH⊥AF,
∴DF2=FH×FA,
即DF=$\sqrt{\frac{3}{2}×10}$=$\sqrt{15}$.
点评 本题主要考查了折叠问题,菱形的判定和性质以及射影定理的应用,利用射影定理得出DF2=FH×FA是解题答问题(2)的关键.折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,对应边和对应角相等.

练习册系列答案
 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目
18.“天文单位”是天文学中测量距离的基本单位,1天文单位约等于149 600 000千米,149 600 000这个数用科学记数法表示为( )
| A. | 1 496×105 | B. | 1 496×108 | C. | 1.496×105 | D. | 1.496×108 |
2.铁一课间餐种类繁多,深受学生喜爱.这天饭堂在课间的出品有鸡腿、薯饼、鱼丸和鸡柳.某同学就九年级学生对课间餐各类食物的喜爱程度做了抽样调查,制成表格如下:
(1)样本容量是250,a=12%,b=30,c=16%.
(2)若小王和小李商议着一起去买课间餐,若他们对以上四种口味的课间餐喜爱程度相同.请你帮他们算一算他们买了相同课间餐的概率.
| 课间餐种类 | 人类 | 百分比 |
| 鸡腿 | 150 | 60% |
| 薯饼 | 30 | a |
| 鱼丸 | b | 12% |
| 鸡柳 | 40 | c |
(2)若小王和小李商议着一起去买课间餐,若他们对以上四种口味的课间餐喜爱程度相同.请你帮他们算一算他们买了相同课间餐的概率.
 已知,A市到B市的路程为260千米,甲车从A市前往B市运送物资,行驶2小时在M地汽车出现故障,立即通知技术人员乘乙车从A市赶来维修(通知时间忽略不计),乙车到达M地后又经过20分钟修好甲车后以原速原路返回A市,同时甲车以原来1.5倍的速度前往B市,如图是两车距A市的路程y(千米)与甲车所用时间x(小时)之间的函数图象,下列四种说法:
已知,A市到B市的路程为260千米,甲车从A市前往B市运送物资,行驶2小时在M地汽车出现故障,立即通知技术人员乘乙车从A市赶来维修(通知时间忽略不计),乙车到达M地后又经过20分钟修好甲车后以原速原路返回A市,同时甲车以原来1.5倍的速度前往B市,如图是两车距A市的路程y(千米)与甲车所用时间x(小时)之间的函数图象,下列四种说法: 如图:在等腰Rt△ABC中,BD=AE,BF与DE垂直,求证:ED=BF.
如图:在等腰Rt△ABC中,BD=AE,BF与DE垂直,求证:ED=BF.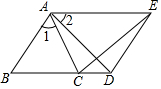 如图,已知∠1=∠2,AB=AC,AD=AE,且B、C、D三点共线.
如图,已知∠1=∠2,AB=AC,AD=AE,且B、C、D三点共线.