题目内容
把分别标有数字2,3,4,5的四个小球放入A袋内,把分别标有数字
,
,
的三个小球放入B袋内,所有小球的形状、大小、质地完全相同,A、B两个袋子不透明.
(1)如果从A袋中摸出的小球上的数字为3,再从B袋中摸出一个小球,两个小球上的数字互为倒数的概率为 ;
(2)小明分别从A,B两个袋子中各摸出一个小球,请用树状图或列表法列出所有可能出现的结果,并求这两个小球上的数字互为倒数的概率.
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 6 |
(1)如果从A袋中摸出的小球上的数字为3,再从B袋中摸出一个小球,两个小球上的数字互为倒数的概率为
(2)小明分别从A,B两个袋子中各摸出一个小球,请用树状图或列表法列出所有可能出现的结果,并求这两个小球上的数字互为倒数的概率.
考点:列表法与树状图法
专题:
分析:(1)由从B袋中摸出一个小球,两个小球上的数字互为倒数的只有
,直接利用概率公式求解即可求得答案;
(2)首先根据题意画出树状图,然后由树状图求得所有等可能的结果与这两个小球上的数字互为倒数的情况,再利用概率公式即可求得答案.
| 1 |
| 3 |
(2)首先根据题意画出树状图,然后由树状图求得所有等可能的结果与这两个小球上的数字互为倒数的情况,再利用概率公式即可求得答案.
解答:解:(1)∵从A袋中摸出的小球上的数字为3,
∴从B袋中摸出一个小球,两个小球上的数字互为倒数的只有
,
∴从B袋中摸出一个小球,两个小球上的数字互为倒数的概率为
.
故答案为:
.
(2)画树状图得:

∵共有12种等可能的结果,这两个小球上的数字互为倒数的只有2种情况,
∴这两个小球上的数字互为倒数的概率为:
=
.
∴从B袋中摸出一个小球,两个小球上的数字互为倒数的只有
| 1 |
| 3 |
∴从B袋中摸出一个小球,两个小球上的数字互为倒数的概率为
| 1 |
| 3 |
故答案为:
| 1 |
| 3 |
(2)画树状图得:

∵共有12种等可能的结果,这两个小球上的数字互为倒数的只有2种情况,
∴这两个小球上的数字互为倒数的概率为:
| 2 |
| 12 |
| 1 |
| 6 |
点评:此题考查了树状图法与列表法求概率.用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
相关题目
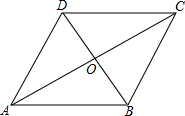 如图所示,四边形ABCD的两条对角线AC、BD相交于点O,AB=
如图所示,四边形ABCD的两条对角线AC、BD相交于点O,AB=
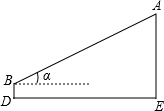 如图,为测量树AE的高,在和E相距a m的D处放测倾器BD,测得树顶A的仰角为α,测倾器高BD=h m,则树高AE为
如图,为测量树AE的高,在和E相距a m的D处放测倾器BD,测得树顶A的仰角为α,测倾器高BD=h m,则树高AE为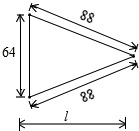 已知一个工件尺寸如图(单位:mm),计算l的长(精确到1mm).
已知一个工件尺寸如图(单位:mm),计算l的长(精确到1mm). 如图,某装置有一枚指针,原来指向南偏西50°,把这枚指针按顺时针方向旋转90°.
如图,某装置有一枚指针,原来指向南偏西50°,把这枚指针按顺时针方向旋转90°.