题目内容
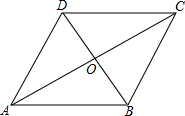如图所示，四边形ABCD的两条对角线AC、BD相交于点O，AB=| 5 |
考点：菱形的判定
专题：证明题
分析：由平行四边形的对角线互相平分得到△AOB的两条边OA、OB的长度，则根据勾股定理的逆定理判定∠AOB=90°，即平行四边形的对角线互相垂直平分，故四边形ABCD是菱形．
解答：证明：∵四边形ABCD是平行四边形，AC=4，BD=2，
∴OA=
AC=2，OB=
BD=1．
又AB=
，
∴AB2=OA2+OB2=5，
∴∠AOB=90°，即AC⊥BD，
∴平行四边形ABCD的对角线互相垂直平分，
∴平行四边形ABCD是菱形．
∴OA=
| 1 |
| 2 |
| 1 |
| 2 |
又AB=
| 5 |
∴AB2=OA2+OB2=5，
∴∠AOB=90°，即AC⊥BD，
∴平行四边形ABCD的对角线互相垂直平分，
∴平行四边形ABCD是菱形．
点评：本题考查了菱形的判定．对角线互相垂直的平行四边形是菱形（或“对角线互相垂直平分的四边形是菱形”）．
练习册系列答案
相关题目
点A（-3，4）关于x轴对称的点的坐标是（ ）
| A、（3，-4） |
| B、（-3，-4） |
| C、（3，4） |
| D、（-4，-3） |
已知：如图，正六边形ABCDEF的边长为2，x轴和y轴是它的两条对称轴．
如图所示，四边形ABCD中，给出下列三个判断：①AD∥BC，②BD2=AD•BC，③∠ABD+∠ADC=180°，请你从其中选取两个条件，另一个做结论构成一个真命题且加以证明．