题目内容
已知,圆O的直径为1,CD⊥AB,M,N分别是CD,BD的中点,求证:cos∠NMD=AC.
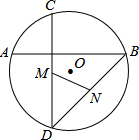

考点:圆周角定理,三角形中位线定理,锐角三角函数的定义
专题:证明题
分析:连接CO并延长交圆于点E,连接AC、BC、AE,利用圆周角定理和直角三角形的性质及中位线定理,可证得∠NMD=∠DCB=∠ACE,又在Rt△ACE中可知cos∠ACE=AC,可证得结论.
解答: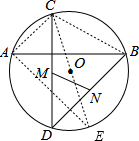 证明:连接CO并延长交圆于E点,连接AC、AE、BC
证明:连接CO并延长交圆于E点,连接AC、AE、BC
∵CE为圆直径,
∴CA⊥AE,
∴cos∠ACE=AC,
∵∠E=∠CBA,且AB⊥CD,
∴∠ACE=∠DCB,
∵M、N为CD、BD的中点,
∴MN∥BC,
∴∠NMD=∠DCB,
∴cos∠NMD=cos∠DCB=cos∠ACE=AC.
 证明:连接CO并延长交圆于E点,连接AC、AE、BC
证明:连接CO并延长交圆于E点,连接AC、AE、BC∵CE为圆直径,
∴CA⊥AE,
∴cos∠ACE=AC,
∵∠E=∠CBA,且AB⊥CD,
∴∠ACE=∠DCB,
∵M、N为CD、BD的中点,
∴MN∥BC,
∴∠NMD=∠DCB,
∴cos∠NMD=cos∠DCB=cos∠ACE=AC.
点评:本题主要考查圆周角定理及三角函数的定义,证明∠NMD=∠DCB=∠ACE,把所求角转化到Rt△ACE中利用三角函数定义是解题的关键.

练习册系列答案
相关题目
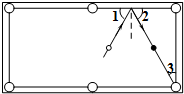 在长方形台球桌上打台球时,球的反射角∠1等于入射角∠2,如图所示.如果∠3=30°,为了使白球反弹后能将黑球直接撞入袋中,那么击打白球时,必须保证∠1的度数为( )
在长方形台球桌上打台球时,球的反射角∠1等于入射角∠2,如图所示.如果∠3=30°,为了使白球反弹后能将黑球直接撞入袋中,那么击打白球时,必须保证∠1的度数为( )| A、30° | B、45° |
| C、60° | D、75° |
某物品的标价为132元,若以9折出售,仍可获利10%,则该物品的进价是( )
| A、118元 | B、108元 |
| C、106元 | D、104元 |
 如图所示,四边形ABCD中,给出下列三个判断:①AD∥BC,②BD2=AD•BC,③∠ABD+∠ADC=180°,请你从其中选取两个条件,另一个做结论构成一个真命题且加以证明.
如图所示,四边形ABCD中,给出下列三个判断:①AD∥BC,②BD2=AD•BC,③∠ABD+∠ADC=180°,请你从其中选取两个条件,另一个做结论构成一个真命题且加以证明. 如图,四个圆的半径都是1,顺次连接四个圆心得到四边形ABCD,则图中阴影部分的面积之和是
如图,四个圆的半径都是1,顺次连接四个圆心得到四边形ABCD,则图中阴影部分的面积之和是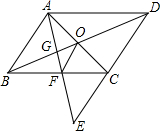 如图,E为?ABCD中DC边的延长线上一点,CE=CD,AE交BC于F,AC交BD于O,连接OF.
如图,E为?ABCD中DC边的延长线上一点,CE=CD,AE交BC于F,AC交BD于O,连接OF.