题目内容
5.如图1,在平面直角坐标系中,点O为坐标原点,抛物线y=x2+bx-3与x轴相交于点A(-3,0)和点B,与y轴相交于点C.(1)求抛物线的解析式;
(2)如图2,直线y=kx+3k经过点A,与y轴正半轴相交于点D,点P为第三象限内抛物线上一点,连接PD绕点P逆时针旋转,与线段AD相交于点E,且∠EPD=2∠PDC,若∠AEP+∠ADP=90°,求点D的坐标;
(3)如图3,在(2)的条件下,过点E作EF⊥PD,垂足为点G,EF与y轴相交于点F,连接PF,若sin∠PFC=$\frac{1}{3}$,求PF的长.
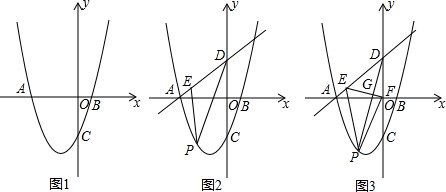
分析 (1)直接把A点坐标代入y=x2+bx-3求出b的值即可得到抛物线解析式为y=x2+2x-3;
(2)如图2,由三角形外角性质得∠AEP=∠2+∠3,加上∠3=2∠1,则∠AEP=∠2+2∠1,再利用∠AEP+∠2=90°可∠1+∠2=45°,于是可判断△AOD为等腰直角三角形,则OD=OA=3,由此得到D点坐标为(0,3);
(3)过D作DH⊥y轴交PE的延长线于H,作PM⊥DH于M,PN⊥y轴于N,如图3,利用PM∥DN得到∠PDC=∠DPM,加上∠EPD=2∠PDC,则∠HPM=∠DPM,于是根据等腰三角形的性质可得MH=MD,接着判断四边形PNDM为矩形得到MD=PN,则DH=2PN,然后证明△DEH≌△DEF得到DH=DF,所以DF=2MD=2PN;再在Rt△PFN中利用正弦定义可得到PF=3PN,利用勾股定理得FN=$\sqrt{2}$PN,设P点坐标为(t,t2+2t-3),则DF=-2t,FN=-2$\sqrt{2}$t,于是可表示出ON=DF+FN-OD=-2t-2$\sqrt{2}$t-3,所以-2t-2$\sqrt{2}$t-3=-(t2+2t-3),解方程得到得t1=-$\sqrt{2}$,t2=3$\sqrt{2}$(舍去),所以PF=3PN=3$\sqrt{2}$.
解答 解:(1)把A(-3,0)代入y=x2+bx-3得9-3b-3=0,解得b=2,
所以抛物线解析式为y=x2+2x-3;
(2)如图2,∵∠AEP=∠2+∠3,
而∠3=2∠1,
∴∠AEP=∠2+2∠1,
∵∠AEP+∠2=90°,
∴∠2+2∠1+∠2=90°,
∴∠1+∠2=45°,即∠ADO=45°,
∴△AOD为等腰直角三角形,
∴OD=OA=3,
∴D点坐标为(0,3);
(3)过D作DH⊥y轴交PE的延长线于H,作PM⊥DH于M,PN⊥y轴于N,如图3,
∵PM∥DN,
∴∠PDC=∠DPM,
∵∠EPD=2∠PDC,
∴∠HPM=∠DPM,
而PM⊥DH,
∴MH=MD,
易得四边形PNDM为矩形,
∴MD=PN,
∴DH=2PN,
∵EF⊥PD,
∴∠GDF+∠DFG=90°,
而∠PHD+∠HPM=90°,
∴∠DFG=∠PHM,
∵∠ADF=45°,
∴∠HDE=45°,
在△DEH和△DEF中
$\left\{\begin{array}{l}{∠H=∠DFE}\\{∠HDE=∠FDE}\\{DE=DE}\end{array}\right.$,
∴△DEH≌△DEF,
∴DH=DF,
∴DF=2MD=2PN,
在Rt△PFN中,∵sin∠PFC=$\frac{PN}{PF}$=$\frac{1}{3}$,
∴PF=3PN,
∴FN=$\sqrt{P{F}^{2}-P{N}^{2}}$=$\sqrt{9P{N}^{2}-P{N}^{2}}$=2$\sqrt{2}$PN,
设P点坐标为(t,t2+2t-3),则DF=-2t,FN=-2$\sqrt{2}$t,
∴ON=DF+FN-OD=-2t-2$\sqrt{2}$t-3,
∴-2t-2$\sqrt{2}$t-3=-(t2+2t-3),
整理得t1=-$\sqrt{2}$,t2=3$\sqrt{2}$(舍去),
∴PF=3PN=-3t=3$\sqrt{2}$.
点评 本题考查了二次函数的综合题:熟练掌握二次函数图象上点的坐标特征和等腰三角形的性质;会应用三角形全等证明线段相等;理解锐角三角函数的定义.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | 在平面内,确定一个物体的位置一般需要两个数据 | |
| B. | 如果两条直线被第三条直线所截,那么内错角相等 | |
| C. | 三角形的一个外角大于任何一个和它不相邻的内角 | |
| D. | 无限不循环小数称为无理数 |

| A. | ① | B. | ①② | C. | ①②③ | D. | ①③④ |
| A. | 也扩大2倍 | B. | 缩小为原来的$\frac{1}{2}$ | C. | 都不变 | D. | 不能确定 |
 如图,是一个正方体的表面展开图,则原正方体中“梦”字所在的面相对的面上标的字是( )
如图,是一个正方体的表面展开图,则原正方体中“梦”字所在的面相对的面上标的字是( )| A. | 伟 | B. | 大 | C. | 的 | D. | 国 |
 如图,阴影部分四边形的两个顶点依次在x轴上,其中横坐标分别为1、3、5的顶点A1、A2、A3在一次函数y=2x+5的图象上,横坐标分别为1、3、5的顶点B1、B2、B3在一次函数y=x+3的图象上,记第一个阴影部分四边形面积为S1,第二个阴影部分四边形面积为S2,第三个阴影部分面积为S3,…,则第2015个阴影部分四边形的面积是( )
如图,阴影部分四边形的两个顶点依次在x轴上,其中横坐标分别为1、3、5的顶点A1、A2、A3在一次函数y=2x+5的图象上,横坐标分别为1、3、5的顶点B1、B2、B3在一次函数y=x+3的图象上,记第一个阴影部分四边形面积为S1,第二个阴影部分四边形面积为S2,第三个阴影部分面积为S3,…,则第2015个阴影部分四边形的面积是( )