题目内容
7.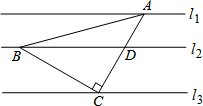 如图,直线l1∥l2∥l3,且l1与l3之间的距离为$\sqrt{3}$,l2与l3之间的距离为1.若点A,B,C分别在直线l1,l2,l3上,且AC⊥BC,AC=BC,AC与直线l2交于点D,则BD的长为$\frac{4\sqrt{3}}{3}$.
如图,直线l1∥l2∥l3,且l1与l3之间的距离为$\sqrt{3}$,l2与l3之间的距离为1.若点A,B,C分别在直线l1,l2,l3上,且AC⊥BC,AC=BC,AC与直线l2交于点D,则BD的长为$\frac{4\sqrt{3}}{3}$.
分析 分别过点A、B、D作AF⊥l3,BE⊥l3,DG⊥l3,先根据全等三角形的判定定理得出△BCE≌△ACF,故可得出CF及CE的长,在Rt△ACF中根据勾股定理求出AC的长,再由相似三角形的判定得出△CDG∽△CAF,故可得出CD的长,在Rt△BCD中根据勾股定理即可求出BD的长.
解答  解:分别过点A、B、D作AF⊥l3,BE⊥l3,DG⊥l3,
解:分别过点A、B、D作AF⊥l3,BE⊥l3,DG⊥l3,
∵△ABC是等腰直角三角形,
∴AC=BC,
∵∠EBC+∠BCE=90°,∠BCE+∠ACF=90°,∠ACF+∠CAF=90°,
∴∠EBC=∠ACF,∠BCE=∠CAF,
在△BCE与△ACF中,
$\left\{\begin{array}{l}{∠EBC=∠ACF}\\{BC=AC}\\{∠BCE=∠CAF}\end{array}\right.$,
∴△BCE≌△ACF(ASA)
∴CF=BE,CE=AF,
∵l1与l2的距离为1,l2与l3的距离为$\sqrt{3}$,
∴CF=BE=1,CE=AF=$\sqrt{3}$,
在Rt△ACF中,
∵AF=$\sqrt{3}$,CF=1,
∴AC=$\sqrt{A{F}^{2}+C{F}^{2}}$=2,
∵AF⊥l3,DG⊥l3,
∴△CDG∽△CAF,
∴$\frac{DG}{AF}$=$\frac{CD}{AC}$,$\frac{1}{\sqrt{3}}=\frac{CD}{2}$,解得CD=$\frac{2\sqrt{3}}{3}$,
在Rt△BCD中,BD=$\sqrt{B{C}^{2}+C{D}^{2}}$=$\frac{4\sqrt{3}}{3}$.
故答案为:$\frac{4\sqrt{3}}{3}$.
点评 本题考查的是全等三角形的判定和性质,相似三角形的判定与性质,根据题意作出辅助线,构造出相似三角形是解答此题的关键.

 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案 如图,矩形ABCD的两边BC、CD分别在x轴、y轴上,点C与原点重合,点A(-1,2),将矩形ABCD沿x轴向右翻滚,经过一次翻滚点A对应点记为A1,经过第二次翻滚点A对应点记为A2…依此类推,经过5次翻滚后点A对应点A5的坐标为( )
如图,矩形ABCD的两边BC、CD分别在x轴、y轴上,点C与原点重合,点A(-1,2),将矩形ABCD沿x轴向右翻滚,经过一次翻滚点A对应点记为A1,经过第二次翻滚点A对应点记为A2…依此类推,经过5次翻滚后点A对应点A5的坐标为( )| A. | (5,2) | B. | (6,0) | C. | (8,0) | D. | (8,1) |
| A. | x=$\frac{5}{2}$ | B. | x=-7 | C. | x1=$\frac{5}{2}$,x2=-7 | D. | 以上都不对 |
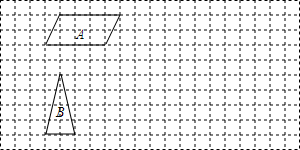
 如图是由7个完全相同的小立方块搭成的几何体,已知每个小立方块的棱长为2cm.
如图是由7个完全相同的小立方块搭成的几何体,已知每个小立方块的棱长为2cm.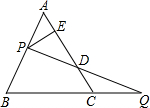 如图,过边长为6的等边△ABC的边AB上一点P,作PE⊥AC于E,Q为BC延长线上一点,当PA=CQ时,连PQ交AC边于D,则DE的长为( )
如图,过边长为6的等边△ABC的边AB上一点P,作PE⊥AC于E,Q为BC延长线上一点,当PA=CQ时,连PQ交AC边于D,则DE的长为( )