题目内容
16.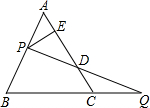 如图,过边长为6的等边△ABC的边AB上一点P,作PE⊥AC于E,Q为BC延长线上一点,当PA=CQ时,连PQ交AC边于D,则DE的长为( )
如图,过边长为6的等边△ABC的边AB上一点P,作PE⊥AC于E,Q为BC延长线上一点,当PA=CQ时,连PQ交AC边于D,则DE的长为( )| A. | 2 | B. | 3 | C. | 4 | D. | 不能确定 |
分析 过P作BC的平行线,交AC于M;则△APM也是等边三角形,在等边三角形APM中,PE是AM上的高,根据等边三角形三线合一的性质知AE=EM;易证得△PMD≌△QCD,则DM=CD;此时发现DE的长正好是AC的一半,由此得解.
解答  解:过P作PM∥BC,交AC于M;
解:过P作PM∥BC,交AC于M;
∵△ABC是等边三角形,且PM∥BC,
∴△APM是等边三角形;
又∵PE⊥AM,
∴AE=EM=$\frac{1}{2}$AM;(等边三角形三线合一)
∵PM∥CQ,
∴∠PMD=∠QCD,∠MPD=∠Q;
又∵PA=PM=CQ,
在△PMD和△QCD中,
$\left\{\begin{array}{l}{∠PDM=∠CDQ}\\{∠PMD=∠DCQ}\\{PM=CQ}\end{array}\right.$,
∴△PMD≌△QCD(AAS);
∴CD=DM=$\frac{1}{2}$CM;
∴DE=DM+ME=$\frac{1}{2}$(AM+MC)=$\frac{1}{2}$AC=3.
故选B.
点评 此题考查了平行线的性质、等边三角形的性质、全等三角形的判定和性质;能够正确的构建出等边三角形△APM是解答此题的关键.

练习册系列答案
相关题目
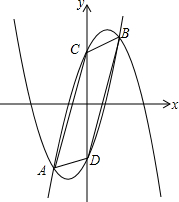 已知,如图,抛物线l1:y=-x2+2x+3与抛物线l2:y=x2+2x-3相交于点A,B,它们分别与y轴相交于C,D,其中点A的横坐标比点B的横坐标小.
已知,如图,抛物线l1:y=-x2+2x+3与抛物线l2:y=x2+2x-3相交于点A,B,它们分别与y轴相交于C,D,其中点A的横坐标比点B的横坐标小.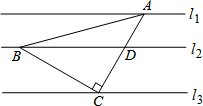 如图,直线l1∥l2∥l3,且l1与l3之间的距离为$\sqrt{3}$,l2与l3之间的距离为1.若点A,B,C分别在直线l1,l2,l3上,且AC⊥BC,AC=BC,AC与直线l2交于点D,则BD的长为$\frac{4\sqrt{3}}{3}$.
如图,直线l1∥l2∥l3,且l1与l3之间的距离为$\sqrt{3}$,l2与l3之间的距离为1.若点A,B,C分别在直线l1,l2,l3上,且AC⊥BC,AC=BC,AC与直线l2交于点D,则BD的长为$\frac{4\sqrt{3}}{3}$. 如图,四边形ABCD的对角线AC与BD相交于点O,∠1=∠2,∠3=∠4.
如图,四边形ABCD的对角线AC与BD相交于点O,∠1=∠2,∠3=∠4.