题目内容
我国中东部地区雾霾天气趋于严重,环境治理已刻不容缓.我市某电器商场根据民众健康需要,代理销售某种家用空气净化器,其进价是200元/台.经过市场销售后发现:在一个月内,当售价是400元/台时,可售出200台,且售价每降低10元,就可多售出50台.若供货商规定这种空气净化器售价不能低于330元/台,代理销售商每月要完成不低于400台的销售任务.
(1)试确定月销售量y(台)与售价x(元/台)之间的函数关系式;并求出自变量x的取值范围;
(2)当售价x(元/台)定为多少时,商场每月销售这种空气净化器所获得的利润w(元)最大?最大利润是多少?
(1)试确定月销售量y(台)与售价x(元/台)之间的函数关系式;并求出自变量x的取值范围;
(2)当售价x(元/台)定为多少时,商场每月销售这种空气净化器所获得的利润w(元)最大?最大利润是多少?
考点:二次函数的应用
专题:
分析:(1)根据题中条件销售价每降低10元,月销售量就可多售出50台,即可列出函数关系式;
根据供货商规定这种空气净化器售价不能低于330元/台,代理销售商每月要完成不低于400台的销售即可求出x的取值.
(2)用x表示y,然后再用x来表示出w,根据函数关系式,即可求出最大w;
根据供货商规定这种空气净化器售价不能低于330元/台,代理销售商每月要完成不低于400台的销售即可求出x的取值.
(2)用x表示y,然后再用x来表示出w,根据函数关系式,即可求出最大w;
解答:解:(1)根据题中条件销售价每降低10元,月销售量就可多售出50台,
则月销售量y(台)与售价x(元/台)之间的函数关系式:y=200+50×
,
化简得:y=-5x+2200;
供货商规定这种空气净化器售价不能低于330元/台,代理销售商每月要完成不低于400台,
则
,
解得:330≤x≤360.
故y与x之间的函数关系式为:y=-5x+2200(330≤x≤360);
(2)W=(x-200)(-5x+2200),
整理得:W=-5(x-320)2+72000.
∵x=320在330≤x≤360内,
∴当x=330时,最大值为71500,
即售价定为330元/台时,商场每月销售这种空气净化器所获得的利润w最大,最大利润是71500元.
则月销售量y(台)与售价x(元/台)之间的函数关系式:y=200+50×
| 400-x |
| 10 |
化简得:y=-5x+2200;
供货商规定这种空气净化器售价不能低于330元/台,代理销售商每月要完成不低于400台,
则
|
解得:330≤x≤360.
故y与x之间的函数关系式为:y=-5x+2200(330≤x≤360);
(2)W=(x-200)(-5x+2200),
整理得:W=-5(x-320)2+72000.
∵x=320在330≤x≤360内,
∴当x=330时,最大值为71500,
即售价定为330元/台时,商场每月销售这种空气净化器所获得的利润w最大,最大利润是71500元.
点评:本题主要考查对于一次函数应用和二次函数应用,注意应用函数变形求函数极值的知识.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
已知a、b为有理数,则多项式a2+b2-2a-6b+12的值为( )
| A、正数 | B、零 | C、负数 | D、非负数 |
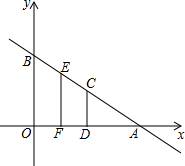 如图,平面直角坐标系中,直线AB解析式为:y=
如图,平面直角坐标系中,直线AB解析式为:y=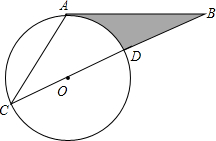 如图所示,AB相切⊙O于点A,直线BO交⊙O于点C、D,且OD=BD,AB=3
如图所示,AB相切⊙O于点A,直线BO交⊙O于点C、D,且OD=BD,AB=3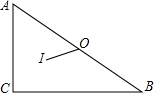 如图,△ABC中,∠C=90°,AC=3,BC=4,O为△ABC的外心,I为△ABC的内心,求OI的长.
如图,△ABC中,∠C=90°,AC=3,BC=4,O为△ABC的外心,I为△ABC的内心,求OI的长.