题目内容
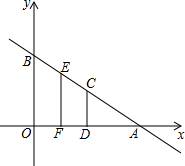 如图,平面直角坐标系中,直线AB解析式为:y=-
如图,平面直角坐标系中,直线AB解析式为:y=-
| ||
| 3 |
| 3 |
(1)写出线段OA、OB的长度,OA=
(2)若点C是AB的中点,过点C作CD⊥x轴于点D,E、F分别为BC、OD的中点,求点E的坐标;
(3)在第一象限内是否存在点P,使得以P、O、B为顶点的三角形与△OBA相似?若存在,请求出所有符合条件的点P的坐标;若不存在,请说明理由.
考点:一次函数综合题
专题:压轴题
分析:(1)令y=0求出x的值即可得到OA,令x=0求出y,即可得到OB;
(2)根据三角形的中位线平行于第三边并且等于第三边的一半求出CD,再根据梯形的中位线等于两底和的一半求出EF,再求出OF,然后写出点E的坐标即可;
(3)根据直线解析式求出∠ABO=60°,再分①∠PBO=90°时,分∠POB=30°和60°两种情况求出PB,然后写出点P的坐标;②∠PBO=60°时,点P在直线AB上,写出直线OP的解析式,然后联立两直线解析式求解即可;③∠PBO=30°时,写出直线PB和直线OP的解析式,然后联立两直线解析式求解即可.
(2)根据三角形的中位线平行于第三边并且等于第三边的一半求出CD,再根据梯形的中位线等于两底和的一半求出EF,再求出OF,然后写出点E的坐标即可;
(3)根据直线解析式求出∠ABO=60°,再分①∠PBO=90°时,分∠POB=30°和60°两种情况求出PB,然后写出点P的坐标;②∠PBO=60°时,点P在直线AB上,写出直线OP的解析式,然后联立两直线解析式求解即可;③∠PBO=30°时,写出直线PB和直线OP的解析式,然后联立两直线解析式求解即可.
解答:解:(1)令y=0,则-
x+
=0,
解得x=3,
所以,OA=3,
令x=0,则y=
,
所以,OB=
;
故答案为:3,
;
(2)∵点C是AB的中点,CD⊥x轴于点D,
∴CD是△AOB的中位线,
∴CD=
OB=
,OD=
OA=
,
∵E、F分别为BC、OD的中点,
∴EF是梯形OBCD的中位线,
∴EF=
×(
+
)=
,
OF=
OD=
,
∴点E的坐标为(
,
);
(3)∵直线AB的解析式为y=-
x+
,
∴∠ABO=60°,∠OAB=30°,
①∠PBO=90°时,若∠POB=30°,则BP=OB•tan30°=
×
=1,
若∠POB=60°,则BP=OB•tan60°=
×
=3,
所以,点P的坐标为(1,
)或(3,
);
②∠PBO=60°时,点P在直线AB上,
此时,直线OP的解析式为y=
x,
联立
,
解得
,
此时,点P的坐标为(
,
);
③∠PBO=30°时,直线PB的解析式为y=-
x+
,
直线OP的解析式的解析式为y=
x,
联立
,
解得
,
此时,点P的坐标为(
,
),
综上所述,在第一象限内存在点P(1,
)或(3,
)或(
,
)或(
,
)使以P、O、B为顶点的三角形与△OBA相似.
| ||
| 3 |
| 3 |
解得x=3,
所以,OA=3,
令x=0,则y=
| 3 |
所以,OB=
| 3 |
故答案为:3,
| 3 |
(2)∵点C是AB的中点,CD⊥x轴于点D,
∴CD是△AOB的中位线,
∴CD=
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
∵E、F分别为BC、OD的中点,
∴EF是梯形OBCD的中位线,
∴EF=
| 1 |
| 2 |
| ||
| 2 |
| 3 |
3
| ||
| 4 |
OF=
| 1 |
| 2 |
| 3 |
| 4 |
∴点E的坐标为(
| 3 |
| 4 |
3
| ||
| 4 |
(3)∵直线AB的解析式为y=-
| ||
| 3 |
| 3 |
∴∠ABO=60°,∠OAB=30°,
①∠PBO=90°时,若∠POB=30°,则BP=OB•tan30°=
| 3 |
| ||
| 3 |
若∠POB=60°,则BP=OB•tan60°=
| 3 |
| 3 |
所以,点P的坐标为(1,
| 3 |
| 3 |
②∠PBO=60°时,点P在直线AB上,
此时,直线OP的解析式为y=
| 3 |
联立
|
解得
|
此时,点P的坐标为(
| 3 |
| 4 |
3
| ||
| 4 |
③∠PBO=30°时,直线PB的解析式为y=-
| 3 |
| 3 |
直线OP的解析式的解析式为y=
| ||
| 3 |
联立
|
解得
|
此时,点P的坐标为(
| 3 |
| 4 |
| ||
| 4 |
综上所述,在第一象限内存在点P(1,
| 3 |
| 3 |
| 3 |
| 4 |
3
| ||
| 4 |
| 3 |
| 4 |
| ||
| 4 |
点评:本题是一次函数综合题型,主要利用了一次函数与坐标轴的交点的求解,三角形的中位线平行于第三边并且等于第三边的一半,梯形的中位线等于两底和的一半,相似三角形的性质,难点在于(3)根据相似三角形对应角相等分情况讨论.

练习册系列答案
 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目
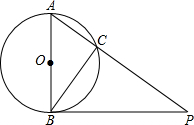 如图,已知AB是⊙O的直径,PB是⊙O的切线,PA交⊙O于C,AB=3cm,PB=4cm,则BC长为( )
如图,已知AB是⊙O的直径,PB是⊙O的切线,PA交⊙O于C,AB=3cm,PB=4cm,则BC长为( ) | A、5cm | B、2.4cm |
| C、3.6cm | D、1.8cm |
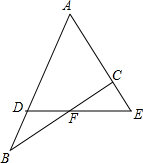 如图所示,已知AD:DB=7:2,AC:CE=4:3,则BF:FC=
如图所示,已知AD:DB=7:2,AC:CE=4:3,则BF:FC=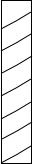 如图,有一根高为2m的圆柱形木材,它的底面周长为0.3m.为了营造喜庆的气氛,小颖想用一根彩带从圆木的底向顶均匀地缠绕7圈,一直缠到起点的正上方为止.小颖至少要准备多长的一根彩带?
如图,有一根高为2m的圆柱形木材,它的底面周长为0.3m.为了营造喜庆的气氛,小颖想用一根彩带从圆木的底向顶均匀地缠绕7圈,一直缠到起点的正上方为止.小颖至少要准备多长的一根彩带?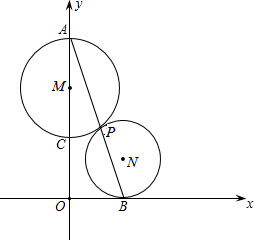 如图,⊙M与⊙N切于点P,经过点P的直线AB交⊙M于点A,交⊙N于点B,以经过⊙M直径AC所在直线为y轴,经过点B的直线为x轴建立平面直角坐标系,
如图,⊙M与⊙N切于点P,经过点P的直线AB交⊙M于点A,交⊙N于点B,以经过⊙M直径AC所在直线为y轴,经过点B的直线为x轴建立平面直角坐标系,