题目内容
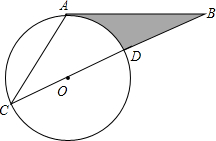 如图所示,AB相切⊙O于点A,直线BO交⊙O于点C、D,且OD=BD,AB=3
如图所示,AB相切⊙O于点A,直线BO交⊙O于点C、D,且OD=BD,AB=3| 3 |
(1)求⊙O的半径;
(2)求∠ABC的度数;
(3)求图中阴影部分的面积.
考点:切线的性质,扇形面积的计算
专题:计算题
分析:(1)连接OA,如图,设⊙O的半径为r,则OD=BD=r,根据切线的性质得OA⊥AB,在Rt△ABO中根据勾股定理得r2+(3
)2=(2r)2,解得r=3;
(2)在Rt△ABO中,由于OA=3,OB=6,根据含30度的直角三角形三边的关系得∠ABO=30°;
(3)先利用互余得∠AOB=60°,然后根据扇形的面积公式和S阴影部分=S△ABO-S扇形AOD进行计算.
| 3 |
(2)在Rt△ABO中,由于OA=3,OB=6,根据含30度的直角三角形三边的关系得∠ABO=30°;
(3)先利用互余得∠AOB=60°,然后根据扇形的面积公式和S阴影部分=S△ABO-S扇形AOD进行计算.
解答:解: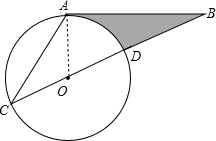 (1)连接OA,如图,设⊙O的半径为r,则OD=BD=r,
(1)连接OA,如图,设⊙O的半径为r,则OD=BD=r,
∵AB相切⊙O于点A,
∴OA⊥AB,
在Rt△ABO中,∵OA2+AB2=OB2,
∴r2+(3
)2=(2r)2,解得r=3,
∴⊙O的半径为3;
(2)在Rt△ABO中,∵OA=3,OB=6,
∴∠ABO=30°,
即∠ABC的度数为30°;
(3)∵∠ABO=30°,
∴∠AOB=60°,
∴S阴影部分=S△ABO-S扇形AOD
=
•3•3
-
=
-
.
 (1)连接OA,如图,设⊙O的半径为r,则OD=BD=r,
(1)连接OA,如图,设⊙O的半径为r,则OD=BD=r,∵AB相切⊙O于点A,
∴OA⊥AB,
在Rt△ABO中,∵OA2+AB2=OB2,
∴r2+(3
| 3 |
∴⊙O的半径为3;
(2)在Rt△ABO中,∵OA=3,OB=6,
∴∠ABO=30°,
即∠ABC的度数为30°;
(3)∵∠ABO=30°,
∴∠AOB=60°,
∴S阴影部分=S△ABO-S扇形AOD
=
| 1 |
| 2 |
| 3 |
| 60•π•32 |
| 360 |
=
9
| ||
| 2 |
| 3π |
| 2 |
点评:本题考查了切线的性质:圆的切线垂直于经过切点的半径.也考查了含30度的直角三角形三边的关系和扇形的面积公式.

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目
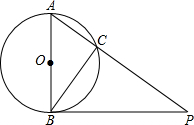 如图,已知AB是⊙O的直径,PB是⊙O的切线,PA交⊙O于C,AB=3cm,PB=4cm,则BC长为( )
如图,已知AB是⊙O的直径,PB是⊙O的切线,PA交⊙O于C,AB=3cm,PB=4cm,则BC长为( ) | A、5cm | B、2.4cm |
| C、3.6cm | D、1.8cm |
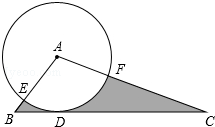 如图,在△ABC中,BC=6,以点A为圆心,2为半径的⊙A与BC相切于点D,交AB于点E,交AC于点F,∠EAF=120°,则图中阴影部分的面积是
如图,在△ABC中,BC=6,以点A为圆心,2为半径的⊙A与BC相切于点D,交AB于点E,交AC于点F,∠EAF=120°,则图中阴影部分的面积是 如图,在Rt△ABC中,CD是斜边AB上的中线,若CD=5,AC=6,则tan∠BCD的值是
如图,在Rt△ABC中,CD是斜边AB上的中线,若CD=5,AC=6,则tan∠BCD的值是 如图,已知点D在线段BE上,且
如图,已知点D在线段BE上,且