题目内容
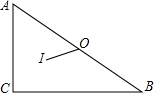 如图,△ABC中,∠C=90°,AC=3,BC=4,O为△ABC的外心,I为△ABC的内心,求OI的长.
如图,△ABC中,∠C=90°,AC=3,BC=4,O为△ABC的外心,I为△ABC的内心,求OI的长.考点:三角形的内切圆与内心,三角形的外接圆与外心
专题:
分析:作OD⊥AC于点D,IE⊥AC于点E,IF⊥BC于点F,交OD于点G.则四边形IECF是正方形,四边形IEDG是矩形.OD是△ABC的中位线,求得内切圆的半径,然后在直角△OGI中利用勾股定理即可求解.
解答: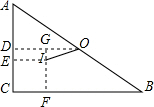 解:作OD⊥AC于点D,IE⊥AC于点E,IF⊥BC于点F,交OD于点G.
解:作OD⊥AC于点D,IE⊥AC于点E,IF⊥BC于点F,交OD于点G.
则四边形IECF是正方形,四边形IEDG是矩形.
则IE=CE=CF=IF=
=1,
∵O是外心,
∴OA=OB,
∴OD是△ABC的中位线,
∴OD=
BC=
×4=2,CD=
AC=
,
∴OG=2-1=1,GI=
-1=
.
在直角△OGI中,OI=
=
=
.
 解:作OD⊥AC于点D,IE⊥AC于点E,IF⊥BC于点F,交OD于点G.
解:作OD⊥AC于点D,IE⊥AC于点E,IF⊥BC于点F,交OD于点G.则四边形IECF是正方形,四边形IEDG是矩形.
则IE=CE=CF=IF=
| 3×4 |
| 3+4+5 |
∵O是外心,
∴OA=OB,
∴OD是△ABC的中位线,
∴OD=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
∴OG=2-1=1,GI=
| 3 |
| 2 |
| 1 |
| 2 |
在直角△OGI中,OI=
| OG2+GI2 |
12+(
|
| ||
| 2 |
点评:本题考查了三角形的内切圆,以及勾股定理,正确作出辅助线是关键.

练习册系列答案
相关题目
 有理数a,b,c在数轴上的位置如图所示,下列各式成立的是( )
有理数a,b,c在数轴上的位置如图所示,下列各式成立的是( )| A、c>b>a |
| B、|a|>|b|>|c| |
| C、|c|>|b|>|a| |
| D、|c|>|a|>|b| |
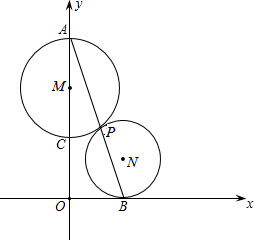 如图,⊙M与⊙N切于点P,经过点P的直线AB交⊙M于点A,交⊙N于点B,以经过⊙M直径AC所在直线为y轴,经过点B的直线为x轴建立平面直角坐标系,
如图,⊙M与⊙N切于点P,经过点P的直线AB交⊙M于点A,交⊙N于点B,以经过⊙M直径AC所在直线为y轴,经过点B的直线为x轴建立平面直角坐标系, 如图,已知点D在线段BE上,且
如图,已知点D在线段BE上,且