题目内容
14.下列说法中正确的是( )| A. | 不相交的两条直线叫做平行线 | |
| B. | 点到直线的距离是这点到直线的垂线段 | |
| C. | 过一点有且只有一条直线与已知直线平行 | |
| D. | 在同一平面内,垂直于同一直线的两直线平行 |
分析 分别利用平行公理以及点到直线的距离以及平行线的判定方法进而得出答案.
解答 解:A、不相交的两条直线叫做平行线,必须在同一平面内,故此选项不合题意;
B、点到直线的距离是这点到直线的垂线段长度,故此选项不合题意;
C、过一点有且只有一条直线与已知直线平行,必须在同一平面内,故此选项不合题意;
D、在同一平面内,垂直于同一直线的两直线平行,正确,符合题意.
故选:D.
点评 此题主要考查了平行公理以及点到直线的距离以及平行线的判定方法等知识,正确把握相关定理与性质是解题关键.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目
4.2617与8213的大小关系是( )
| A. | 2617>8213 | B. | 2617=8213 | C. | 2617<8213 | D. | 不能判定 |
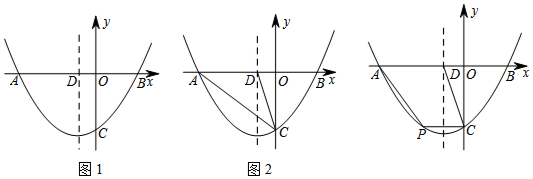
9. 如图,下列条件中,不能判定直线l1∥l2的是( )
如图,下列条件中,不能判定直线l1∥l2的是( )
 如图,下列条件中,不能判定直线l1∥l2的是( )
如图,下列条件中,不能判定直线l1∥l2的是( )| A. | ∠1=∠3 | B. | ∠2+∠4=180° | C. | ∠2=∠3 | D. | ∠4=∠5 |
19.计算:
(1)($\sqrt{3}-1$)0+|-3|-($\frac{1}{2}$)-2+$\sqrt{4}$
(2)$\frac{{x}^{2}}{x-2}$+$\frac{4}{2-x}$.
(1)($\sqrt{3}-1$)0+|-3|-($\frac{1}{2}$)-2+$\sqrt{4}$
(2)$\frac{{x}^{2}}{x-2}$+$\frac{4}{2-x}$.
4. 已知某大型超市今年在销售某种水果时,1~6月份的销售单价y1(元/千克)与时间x(月)的关系如表:
已知某大型超市今年在销售某种水果时,1~6月份的销售单价y1(元/千克)与时间x(月)的关系如表:
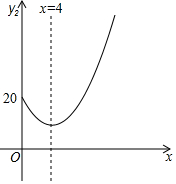
7~10月份的销售单价y2(元/千克)与时间x(月)满足函数关系:y2=x2+bx+c,其图象如图.今年1~6月份的月销量z1(万千克)与时间x(月)满足关系式:z1=-x2+6x;而7~10月份的月销量一直稳定在8万千克.
(1)请观察题目中的表格及图象,直接写出y1(元/千克)与时间x(月)的函数关系式及y2(元/千克)与时间x(月)的函数关系式.
(2)求出该种水果今年1~10月哪个月的销售额最大?最大销售额为多少万元?
(3)进入11月后,商场决定将销售单价在取得最大月销售额时的单价的基础上提高2a%,预测月销售量将在取得最大月销售额时的销售量的基础上下降0.5a%,若要使该种水果11月份的销售额达到360万元,求出a的最小整数值(a<100)?(参考数据:$\sqrt{6}$≈2.45;$\sqrt{7}$≈2.65;$\sqrt{8}$≈2.83)
 已知某大型超市今年在销售某种水果时,1~6月份的销售单价y1(元/千克)与时间x(月)的关系如表:
已知某大型超市今年在销售某种水果时,1~6月份的销售单价y1(元/千克)与时间x(月)的关系如表:| x | 1 | 2 | 3 | 4 | 5 | 6 |
| y1 | 60 | 30 | 20 | 15 | 12 | 10 |
(1)请观察题目中的表格及图象,直接写出y1(元/千克)与时间x(月)的函数关系式及y2(元/千克)与时间x(月)的函数关系式.
(2)求出该种水果今年1~10月哪个月的销售额最大?最大销售额为多少万元?
(3)进入11月后,商场决定将销售单价在取得最大月销售额时的单价的基础上提高2a%,预测月销售量将在取得最大月销售额时的销售量的基础上下降0.5a%,若要使该种水果11月份的销售额达到360万元,求出a的最小整数值(a<100)?(参考数据:$\sqrt{6}$≈2.45;$\sqrt{7}$≈2.65;$\sqrt{8}$≈2.83)
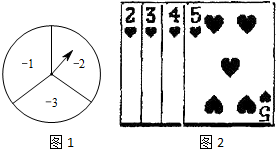 图1是一个可以自由转动的转盘,被分成了面积相等的三个扇形,分别标有数-1,-2,-3,甲转动一次转盘,转盘停止后指针指向的扇形内的数记为A(如果指针恰好指在分割线上,那么重转一次,直到指针指向某一扇形为止).图2背面完全一样、牌面数字分别是2,3,4,5的四张扑克牌,把四张扑克牌背面朝上,洗匀后放在桌面上,乙随机抽出一张牌面数字记为B.计算A+B的值.
图1是一个可以自由转动的转盘,被分成了面积相等的三个扇形,分别标有数-1,-2,-3,甲转动一次转盘,转盘停止后指针指向的扇形内的数记为A(如果指针恰好指在分割线上,那么重转一次,直到指针指向某一扇形为止).图2背面完全一样、牌面数字分别是2,3,4,5的四张扑克牌,把四张扑克牌背面朝上,洗匀后放在桌面上,乙随机抽出一张牌面数字记为B.计算A+B的值.