Question

5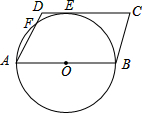．如图，在?ABCD中，AB为⊙O的直径，⊙O与DC相切于点E，与AD相交于点F，已知AB=12，∠C=60°，则$\widehat{FE}$的长为（　　）

• A． $\frac{π}{3}$
• B． $\frac{π}{2}$
• C． π
• D． 2π

Answer 1

分析 首先求出圆心角∠EOF的度数，再根据弧长公式l=$\frac{n•π•R}{180}$，即可解决问题．

解答 解：如图连接OE、OF，

∵CD是⊙O的切线，
∴OE⊥CD，
∴∠OED=90°，
∵四边形ABCD是平行四边形，∠C=60°，
∴∠A=∠C=60°，∠D=120°，
∵OA=OF，
∴∠A=∠OFA=60°，
∴∠DFO=120°，
∴∠EOF=360°-∠D-∠DFO-∠DEO=30°，
$\widehat{EF}$的长=$\frac{30π•6}{180}$=π．
故选C．

点评 本题考查切线的性质、平行四边形的性质、弧长公式等知识，解题的关键是求出圆心角的度数，记住弧长公式，属于中考常考题型．