题目内容
15. 如图,已知点A在函数y=$\frac{k}{x}$(x<0)图象上,过点A作AB∥x轴,且AB交直线y=x于点B,交y轴正半轴于点C.若AB2-AO2=4,则k=-2.
如图,已知点A在函数y=$\frac{k}{x}$(x<0)图象上,过点A作AB∥x轴,且AB交直线y=x于点B,交y轴正半轴于点C.若AB2-AO2=4,则k=-2.
分析 由点A在反比例函数图象上,设出点A的坐标为(m,$\frac{k}{m}$),用含m、k的代数式表示出点B的坐标,再由两点间的距离公式表示出来AB2和AO2,两者做差,即可得出关于k的一元一次方程,解方程即可得出结论.
解答 解:∵点A在反比例函数y=$\frac{k}{x}$(x<0)图象上,
∴设点A的坐标为(m,$\frac{k}{m}$),
将$\frac{k}{m}$代入到y=x中,得:y=$\frac{k}{m}$,
∴点B的坐标为($\frac{k}{m}$,$\frac{k}{m}$).
∵点A(m,$\frac{k}{m}$),点B($\frac{k}{m}$,$\frac{k}{m}$),点O(0,0),
∴AB2=$(\frac{k}{m}-m)^{2}$,AO2=m2+$(\frac{k}{m})^{2}$.
∵AB2-AO2=4,
∴$(\frac{k}{m}-m)^{2}$-m2+$(\frac{k}{m})^{2}$=4,即-2k=4,
解得:k=-2.
故答案为-2.
点评 本题考查了反比例函数与一次函数的交点问题、反比例函数图象上点的坐标特征、两点间的距离公式以及解一元一次方程,解题的关键是根据AB2-AO2=4找出关于k的一元一次方程.本题属于基础题,难度不大,解决该题型题目时,找出点的坐标,根据两点间的距离公式结合已知条件找出关于反比例函数系数k的方程是关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
5.把抛物线y=x2+1向左平移3个单位,再向下平移2个单位,得到的抛物线表达式为( )
| A. | y=(x+3)2-1 | B. | y=(x-3)2-2 | C. | y=(x-3)2+2 | D. | y=(x-3)2-1 |
4.不透明的袋子中装有形状、大小、质地完全相同的6个球,其中4个黑球、2个白球,从袋子中一次摸出3个球,下列事件是不可能事件的是( )
| A. | 摸出的是3个白球 | B. | 摸出的是3个黑球 | ||
| C. | 摸出的是2个白球、1个黑球 | D. | 摸出的是2个黑球、1个白球 |
5.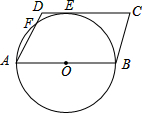 如图,在?ABCD中,AB为⊙O的直径,⊙O与DC相切于点E,与AD相交于点F,已知AB=12,∠C=60°,则$\widehat{FE}$的长为( )
如图,在?ABCD中,AB为⊙O的直径,⊙O与DC相切于点E,与AD相交于点F,已知AB=12,∠C=60°,则$\widehat{FE}$的长为( )
 如图,在?ABCD中,AB为⊙O的直径,⊙O与DC相切于点E,与AD相交于点F,已知AB=12,∠C=60°,则$\widehat{FE}$的长为( )
如图,在?ABCD中,AB为⊙O的直径,⊙O与DC相切于点E,与AD相交于点F,已知AB=12,∠C=60°,则$\widehat{FE}$的长为( )| A. | $\frac{π}{3}$ | B. | $\frac{π}{2}$ | C. | π | D. | 2π |
 如图,在平行四边形ABCD中,∠ABC的平分线交CD于点E,∠ADC的平分线交AB于点F.求证:AF=CE.
如图,在平行四边形ABCD中,∠ABC的平分线交CD于点E,∠ADC的平分线交AB于点F.求证:AF=CE.