题目内容
16.如图,BD是正方形ABCD的对角线,BC=2,边BC在其所在的直线上平移,将通过平移得到的线段记为PQ,连接PA、QD,并过点Q作QO⊥BD,垂足为O,连接OA、OP.(1)请直接写出线段BC在平移过程中,四边形APQD是什么四边形?
(2)请判断OA、OP之间的数量关系和位置关系,并加以证明;
(3)在平移变换过程中,设y=S△OPB,BP=x(0≤x≤2),求y与x之间的函数关系式,并求出y的最大值.

分析 (1)根据平移的性质,可得PQ,根据一组对边平行且相等的四边形是平行四边形,可得答案;
(2)根据正方形的性质,平移的性质,可得PQ与AB的关系,根据等腰直角三角形的判定与性质,可得∠PQO,根据全等三角形的判定与性质,可得AO与OP的数量关系,根据余角的性质,可得AO与OP的位置关系;
(3)根据等腰直角三角形的性质,可得OE的长,根据三角形的面积公式,可得二次函数,根据二次函数的性质,可得到答案.
解答 (1)四边形APQD为平行四边形;
(2)OA=OP,OA⊥OP,理由如下:
∵四边形ABCD是正方形,
∴AB=BC=PQ,∠ABO=∠OBQ=45°,
∵OQ⊥BD,
∴∠PQO=45°,
∴∠ABO=∠OBQ=∠PQO=45°,
∴OB=OQ,
在△AOB和△OPQ中,
$\left\{\begin{array}{l}{AB=PQ}\\{∠ABO=∠PQO}\\{BO=QO}\end{array}\right.$
∴△AOB≌△POQ(SAS),
∴OA=OP,∠AOB=∠POQ,
∴∠AOP=∠BOQ=90°,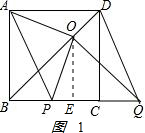
∴OA⊥OP;
(3)如图,过O作OE⊥BC于E.
①如图1,当P点在B点右侧时,
则BQ=x+2,OE=$\frac{x+2}{2}$,
∴y=$\frac{1}{2}$×$\frac{x+2}{2}$•x,即y=$\frac{1}{4}$(x+1)2-$\frac{1}{4}$,
又∵0≤x≤2,
∴当x=2时,y有最大值为2;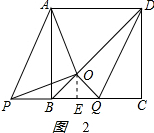
②如图2,当P点在B点左侧时,
则BQ=2-x,OE=$\frac{2-x}{2}$,
∴y=$\frac{1}{2}$×$\frac{2-x}{2}$•x,即y=-$\frac{1}{4}$(x-1)2+$\frac{1}{4}$,
又∵0≤x≤2,
∴当x=1时,y有最大值为$\frac{1}{4}$;
综上所述,∴当x=2时,y有最大值为2;
点评 本题考查了二次函数综合题,利用平行四边形的判定是解题关键;利用全等三角形的判定与性质是解题关键;利用等腰直角三角形的性质的出OE的长是解题关键,又利用了二次函数的性质.

| A. | 摸出的是3个白球 | B. | 摸出的是3个黑球 | ||
| C. | 摸出的是2个白球、1个黑球 | D. | 摸出的是2个黑球、1个白球 |
 如图是由几个相同的小立方块组成的几何体的三视图,小立方块的个数是( )
如图是由几个相同的小立方块组成的几何体的三视图,小立方块的个数是( )| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
| A. | (a-b)2=a2-b2 | B. | (1+a)(a-1)=a2-1 | C. | a2+ab+b2=(a+b)2 | D. | (x+3)2=x2+3x+9 |
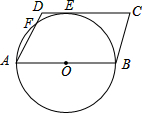 如图,在?ABCD中,AB为⊙O的直径,⊙O与DC相切于点E,与AD相交于点F,已知AB=12,∠C=60°,则$\widehat{FE}$的长为( )
如图,在?ABCD中,AB为⊙O的直径,⊙O与DC相切于点E,与AD相交于点F,已知AB=12,∠C=60°,则$\widehat{FE}$的长为( )| A. | $\frac{π}{3}$ | B. | $\frac{π}{2}$ | C. | π | D. | 2π |
