题目内容
10.若式子$\sqrt{k-1}$+(k-1)0有意义,则一次函数y=(1-k)x+k-1的图象可能是( )| A. |  | B. |  | C. |  | D. |  |
分析 先求出k的取值范围,再判断出1-k及k-1的符号,进而可得出结论.
解答 解:∵式子$\sqrt{k-1}$+(k-1)0有意义,
∴$\left\{\begin{array}{l}k-1≥0\\ k-1≠0\end{array}\right.$,解得k>1,
∴1-k<0,k-1>0,
∴一次函数y=(1-k)x+k-1的图象过一、二、四象限.
故选C.
点评 本题考查的是一次函数的图象,熟知一次函数的图象与系数的关系是解答此题的关键.

练习册系列答案
相关题目
1. 如图是由几个相同的小立方块组成的几何体的三视图,小立方块的个数是( )
如图是由几个相同的小立方块组成的几何体的三视图,小立方块的个数是( )
 如图是由几个相同的小立方块组成的几何体的三视图,小立方块的个数是( )
如图是由几个相同的小立方块组成的几何体的三视图,小立方块的个数是( )| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
5.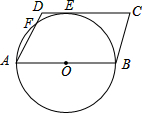 如图,在?ABCD中,AB为⊙O的直径,⊙O与DC相切于点E,与AD相交于点F,已知AB=12,∠C=60°,则$\widehat{FE}$的长为( )
如图,在?ABCD中,AB为⊙O的直径,⊙O与DC相切于点E,与AD相交于点F,已知AB=12,∠C=60°,则$\widehat{FE}$的长为( )
 如图,在?ABCD中,AB为⊙O的直径,⊙O与DC相切于点E,与AD相交于点F,已知AB=12,∠C=60°,则$\widehat{FE}$的长为( )
如图,在?ABCD中,AB为⊙O的直径,⊙O与DC相切于点E,与AD相交于点F,已知AB=12,∠C=60°,则$\widehat{FE}$的长为( )| A. | $\frac{π}{3}$ | B. | $\frac{π}{2}$ | C. | π | D. | 2π |
2. 如图所示,AB∥CD,EF⊥BD,垂足为E,∠1=50°,则∠2的度数为( )
如图所示,AB∥CD,EF⊥BD,垂足为E,∠1=50°,则∠2的度数为( )
 如图所示,AB∥CD,EF⊥BD,垂足为E,∠1=50°,则∠2的度数为( )
如图所示,AB∥CD,EF⊥BD,垂足为E,∠1=50°,则∠2的度数为( )| A. | 50° | B. | 40° | C. | 45° | D. | 25° |
19. 如图,从一张腰长为60cm,顶角为120°的等腰三角形铁皮OAB中剪出一个最大的扇形OCD,用此剪下的扇形铁皮围成一个圆锥的侧面(不计损耗),则该圆锥的高为( )
如图,从一张腰长为60cm,顶角为120°的等腰三角形铁皮OAB中剪出一个最大的扇形OCD,用此剪下的扇形铁皮围成一个圆锥的侧面(不计损耗),则该圆锥的高为( )
 如图,从一张腰长为60cm,顶角为120°的等腰三角形铁皮OAB中剪出一个最大的扇形OCD,用此剪下的扇形铁皮围成一个圆锥的侧面(不计损耗),则该圆锥的高为( )
如图,从一张腰长为60cm,顶角为120°的等腰三角形铁皮OAB中剪出一个最大的扇形OCD,用此剪下的扇形铁皮围成一个圆锥的侧面(不计损耗),则该圆锥的高为( )| A. | 10cm | B. | 15cm | C. | 10$\sqrt{3}$cm | D. | 20$\sqrt{2}$cm |
 如图,在平行四边形ABCD中,∠ABC的平分线交CD于点E,∠ADC的平分线交AB于点F.求证:AF=CE.
如图,在平行四边形ABCD中,∠ABC的平分线交CD于点E,∠ADC的平分线交AB于点F.求证:AF=CE. 如图,在⊙O中,圆心角∠AOB=70°,那么圆周角∠C=35°.
如图,在⊙O中,圆心角∠AOB=70°,那么圆周角∠C=35°. 如图是由四个相同的小正方体组成的几何体,则这个几何体的主视图是( )
如图是由四个相同的小正方体组成的几何体,则这个几何体的主视图是( )



 如图,四边形ABCD是⊙O的内接四边形,若∠B=130°,则∠AOC的大小为100°.
如图,四边形ABCD是⊙O的内接四边形,若∠B=130°,则∠AOC的大小为100°.