题目内容
如图，所有的四边形都是正方形，所有的三角形都是直角三角形，其中最大的正方形的边长为9cm，则正方形A，B，C，D的面积之和为考点：勾股定理
专题：
分析：根据勾股定理有S正方形2+S正方形3=S正方形1，S正方形C+S正方形D=S正方形3，S正方形A+S正方形B=S正方形2，等量代换即可求四个小正方形的面积之和．
解答：
解：如右图所示，
根据勾股定理可知，
S正方形2+S正方形3=S正方形1，
S正方形C+S正方形D=S正方形3，
S正方形A+S正方形B=S正方形2，
∴S正方形C+S正方形D+S正方形A+S正方形B=S正方形2+S正方形3=S正方形1=92=81．
故答案是81．
解：如右图所示，根据勾股定理可知，
S正方形2+S正方形3=S正方形1，
S正方形C+S正方形D=S正方形3，
S正方形A+S正方形B=S正方形2，
∴S正方形C+S正方形D+S正方形A+S正方形B=S正方形2+S正方形3=S正方形1=92=81．
故答案是81．
点评：本题考查了勾股定理的几何意义，关键是掌握两直角边的平方和等于斜边的平方．
练习册系列答案
名校练考卷期末冲刺卷系列答案
相关题目
如图，以原点O为圆心的圆交x轴于A，B两点，交y轴的正半轴于点C，D为第一象限内⊙O上的一点，若∠DAB=30°，求∠OCD．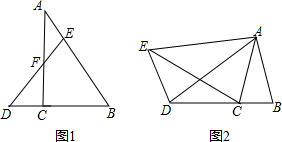
如图，若∠A=70°，∠ABD=120°，则∠ACB=
如图，点O是△ABC的两条垂直平分线的交点，∠BAC=70°，则∠BOC=
如图，A，B，C是⊙O上三点，∠BAC的平分线AM交BC于点D，交⊙O于点M．若∠BAC=60°，∠ABC=50°，则∠CBM=
如图，对于锐角A的每一个确定的值，sinA，cosA，tanA都有唯一确定的值与它对应，所以sinA，cosA，tanA都是A的