题目内容
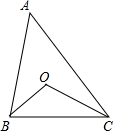
 如图,点O是△ABC的两条垂直平分线的交点,∠BAC=70°,则∠BOC=
如图,点O是△ABC的两条垂直平分线的交点,∠BAC=70°,则∠BOC=考点:线段垂直平分线的性质
专题:
分析:由O是△ABC的两条边垂直平分线的交点,根据线段垂直平分线的性质,可得OA=OB=OC,即可得∠OBA=∠OAB,∠OCA=∠OAC,∠OBC=∠OCB,又由∠BAC=70°,即可求得∠OBC+∠OCB的度数,继而求得答案.
解答:解:∵O是△ABC的两条边垂直平分线的交点,
∴OA=OB=OC,
∴∠OBA=∠OAB,∠OCA=∠OAC,∠OBC=∠OCB,
∵∠BAC=70°,
即∠BAO+∠CAO=∠ABO+∠ACO=70°,
∴∠OBC+∠OCB=180°-2×70°=40°,
∴∠BOC=180°-(∠OBC+∠OCB)=140°,
故答案为:140°.
∴OA=OB=OC,
∴∠OBA=∠OAB,∠OCA=∠OAC,∠OBC=∠OCB,
∵∠BAC=70°,
即∠BAO+∠CAO=∠ABO+∠ACO=70°,
∴∠OBC+∠OCB=180°-2×70°=40°,
∴∠BOC=180°-(∠OBC+∠OCB)=140°,
故答案为:140°.
点评:此题考查了线段垂直平分线的性质以及等腰三角形的性质.此题难度不大,注意掌握数形结合思想的应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,在△ABC中,∠ABC=80°,∠ACB=60°,点O为内心,则∠BOC=
如图,在△ABC中,∠ABC=80°,∠ACB=60°,点O为内心,则∠BOC= 如图,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形的边长为9cm,则正方形A,B,C,D的面积之和为
如图,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形的边长为9cm,则正方形A,B,C,D的面积之和为 如图,直线l上有三个正方形a、b、c,若a、c的面积分别为5和11,则正方形b的边长为
如图,直线l上有三个正方形a、b、c,若a、c的面积分别为5和11,则正方形b的边长为