题目内容
如图，A，B，C是⊙O上三点，∠BAC的平分线AM交BC于点D，交⊙O于点M．若∠BAC=60°，∠ABC=50°，则∠CBM=考点：圆周角定理
专题：
分析：首先在△ABC中利用三角形的内角和定理求得∠BAC的度数，根据角平分线的定义求得∠BAM和∠CAM的度数，然后根据同弧所对的圆周角相等即可求解．
解答：解：∵∠BCA=180°-∠BAC-∠ABC=180°-60°-50°=70°，
∴∠AMB=∠BCA=70°；
∵AM平分∠BAC，
∴∠BAM=∠CAM=33°，
∴∠CBM=∠CAM=30°．
故答案是：30°；70°．
∴∠AMB=∠BCA=70°；
∵AM平分∠BAC，
∴∠BAM=∠CAM=33°，
∴∠CBM=∠CAM=30°．
故答案是：30°；70°．
点评：本题考查了三角形内角和定理以及圆周角定理，同弧所对的圆周角相等．
练习册系列答案
阳光课堂课时作业系列答案
相关题目
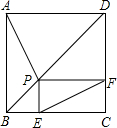如图，正方形ABCD中，P为对角线BD上一点（P点不与B、D重合），PE⊥BC于E，PF⊥DC于F，连接EF，猜想AP与EF的关系并证明你的结论．
如图，所有的四边形都是正方形，所有的三角形都是直角三角形，其中最大的正方形的边长为9cm，则正方形A，B，C，D的面积之和为
与三角形各边都相切的圆叫做三角形的