题目内容
(1)如图1,在△ABC中,∠ACB=90°,点D在BC的延长线上,点E在AB上,DE交AC于点F,ED=EB,求证:AE=EF;
(2)如图2,AB=AC,AD=AE,∠ADE=∠B,求证:BD=CE.
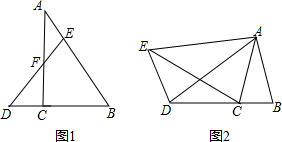
(2)如图2,AB=AC,AD=AE,∠ADE=∠B,求证:BD=CE.

考点:全等三角形的判定与性质,等腰三角形的判定与性质
专题:证明题
分析:(1)根据等边对等角,可得∠B与∠D的关系,根据直角三角形两锐角互余,可得∠B与∠A的关系,∠D与∠DFC的关系,根据根据等角的余角相等,可得∠A与∠AFE的关系,根据等角对等边,可得AE=EF;
(2)根据两边相等的三角形是等腰三角形,可得△ABC与△ADE是等腰三角形,根据等腰三角形顶角相等,可得∠BAC与∠DAE的关系,根据等式的性质,可得∠BAD与∠CAE的关系,根据“SAS”可得△ABD与△ACE的关系,△三角形的性质,可得对应边相等.
(2)根据两边相等的三角形是等腰三角形,可得△ABC与△ADE是等腰三角形,根据等腰三角形顶角相等,可得∠BAC与∠DAE的关系,根据等式的性质,可得∠BAD与∠CAE的关系,根据“SAS”可得△ABD与△ACE的关系,△三角形的性质,可得对应边相等.
解答:证明:(1)∵ED=EB,
∴∠B=∠D(等边对等角).
∵∠ACB=90°,
∴∠B+∠A=90°,∠D+∠DFC=90°(直角三角形两锐角互余).
∵∠AFE=∠DFC(对顶角相等),
∴∠D+∠AFE=90°(等角的余角相等).
∴∠AFE=∠A(等角的余角相等),
∴AE=EF (等角对等边);
(2)∵AB=AC.AD=AE,
∴△ABC与△ADE都是等腰三角形,
∵∠ADE=∠B,
∴∠BAC=180°-2∠B=180°-2∠ADE=∠DAE.(等式的性质)
∠BAC+CAD=∠DAE+CAD(等式的性质)
∠BAD=∠CAE.
在△ABD和△ACE中,
∴△ABD≌△ACE(SAS)
∴BD=CE(全等三角形的对应边相等).
∴∠B=∠D(等边对等角).
∵∠ACB=90°,
∴∠B+∠A=90°,∠D+∠DFC=90°(直角三角形两锐角互余).
∵∠AFE=∠DFC(对顶角相等),
∴∠D+∠AFE=90°(等角的余角相等).
∴∠AFE=∠A(等角的余角相等),
∴AE=EF (等角对等边);
(2)∵AB=AC.AD=AE,
∴△ABC与△ADE都是等腰三角形,
∵∠ADE=∠B,
∴∠BAC=180°-2∠B=180°-2∠ADE=∠DAE.(等式的性质)
∠BAC+CAD=∠DAE+CAD(等式的性质)
∠BAD=∠CAE.
在△ABD和△ACE中,
|
∴△ABD≌△ACE(SAS)
∴BD=CE(全等三角形的对应边相等).
点评:本题考查了全等三角形的性质与判定,(1)先是运用等边对等角,再运用直角三角形两锐角互余,等角的余角相等,最后是等角对等边;(2)等腰三角形的底角相等,顶角相等,运用等式的性质得出∠BAD=∠CAE,“SAS“证明两三角形全等,全等三角形的对应边相等.

练习册系列答案
相关题目
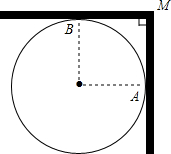 小红家的锅盖坏了,为了配一个锅盖,需要测量锅的直径(锅沿所形成的圆的直径),而小红家只有一把长20cm的直尺,根本不够长,怎么办呢?小红想了想,采取了以下办法:如图,首先把锅平放到墙根,锅沿刚好靠到两墙,用直尺紧贴墙面量得MA的长,即可求出锅的直径.请你利用图说明她这样做的理由.
小红家的锅盖坏了,为了配一个锅盖,需要测量锅的直径(锅沿所形成的圆的直径),而小红家只有一把长20cm的直尺,根本不够长,怎么办呢?小红想了想,采取了以下办法:如图,首先把锅平放到墙根,锅沿刚好靠到两墙,用直尺紧贴墙面量得MA的长,即可求出锅的直径.请你利用图说明她这样做的理由.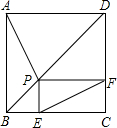 如图,正方形ABCD中,P为对角线BD上一点(P点不与B、D重合),PE⊥BC于E,PF⊥DC于F,连接EF,猜想AP与EF的关系并证明你的结论.
如图,正方形ABCD中,P为对角线BD上一点(P点不与B、D重合),PE⊥BC于E,PF⊥DC于F,连接EF,猜想AP与EF的关系并证明你的结论.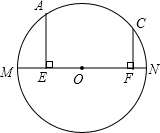 如图,MN=10是⊙O的直径,AE⊥MN于E,CF⊥MN于F,AE=4,CF=3,
如图,MN=10是⊙O的直径,AE⊥MN于E,CF⊥MN于F,AE=4,CF=3, 如图,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形的边长为9cm,则正方形A,B,C,D的面积之和为
如图,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形的边长为9cm,则正方形A,B,C,D的面积之和为