题目内容
4．学习完一次函数后，小荣遇到过这样的一个新颖的函数：y=|x-1|，小荣根据学校函数的经验，对函数y=|x-1|的图象与性质进行了探究．下面是小荣的探究过程，请补充完成：（1）列表：下表是y与x的几组对应值，请补充完整．
| x | … | -3 | -2 | -1 | 0 | 1 | 2 | 3 | … |
| y | … | 4 | 3 | 2 | 1 | 0 | 1 | 2 | … |
（3）进一步探究发现，该函数图象的最低点的坐标是（1，0），结合函数的图象，写出该函数的其他性质（一条即可）：当x＜0时，y随x的增大而减小．
分析 （1）根据y=|x-1|，可以求得表格中缺失的数据，从而可以解答本题；
（2）根据表格中的数据可以在平面直角坐标系中描点，并画出函数的图象；
（3）根据（2）中函数的图象得到该函数的一条性质．
解答 解：（1）∵y=|x-1|，
∴x=-2时，y=3；x=0时，y=1；x=1时，y=0；x=3时，y=2；
故答案为：3；1；0；2；
（2）函数图象如下：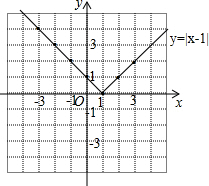
（3）根据第二问的函数图象可知，当x＜1时，y随x的增大而减小，
故答案为：当x＜1时，y随x的增大而减小．
点评 本题考查一次函数的图象和一次函数的性质，解题的关键是明确一次函数图象的画法，根据函数图象可以得到函数的性质，利用数形结合的思想解答问题．
练习册系列答案
相关题目
14．
如图，矩形ABCD的边AB在x轴上，AB的中点与原点O重合，AB=2，AD=1，点Q的坐标为（0，2）．点P（x，0）在边AB上运动，若过点Q、P的直线将矩形ABCD的周长分成2：1两部分，则x的值为（ ）
如图，矩形ABCD的边AB在x轴上，AB的中点与原点O重合，AB=2，AD=1，点Q的坐标为（0，2）．点P（x，0）在边AB上运动，若过点Q、P的直线将矩形ABCD的周长分成2：1两部分，则x的值为（ ）| A． | $\frac{1}{2}$或$-\frac{1}{2}$ | B． | $\frac{1}{3}$或$-\frac{1}{3}$ | C． | $\frac{3}{4}$或$-\frac{3}{4}$ | D． | $\frac{2}{3}$或$-\frac{2}{3}$ |
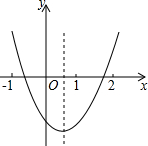如图，观察二次函数y=ax2+bx+c的图象，下列结论：①a+b+c＞0，②2a+b＞0，
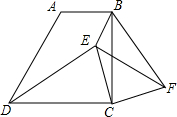在梯形ABCD中AB∥CD，∠BCD=90°，AB=1，BC=2，tan∠ADC=2．