题目内容
已知抛物线y=2x2-8x+m的顶点在x轴上,则m= .
考点:二次函数的性质
专题:
分析:顶点在x轴上,所以顶点的纵坐标是0.根据顶点公式即可求得m的值.
解答:解:抛物线的顶点纵坐标是:
,则
得到:
=0,
解得m=8.
故答案为8.
| 4×2m-64 |
| 4×2 |
得到:
| 4×2m-64 |
| 4×2 |
解得m=8.
故答案为8.
点评:本题考查了二次函数的性质.解答该题时需牢记抛物线y=ax2+bx+c(a≠0)的顶点坐标为(-
,
).
| b |
| 2a |
| 4ac-b2 |
| 4a |

练习册系列答案
相关题目
若等腰三角形的两内角度数比为1:4,则它的顶角为( )度.
| A、36或144 | B、20或120 |
| C、120 | D、20 |
下列说法错误的是( )
| A、过两点有且只有一条直线 |
| B、直线AB和直线BA表示同一条直线 |
| C、两点之间,线段最短 |
| D、AB=BC,则点B是线段AC的中点 |
 如图,已知△ABC中,∠A=75°,则∠1+∠2=( )
如图,已知△ABC中,∠A=75°,则∠1+∠2=( )| A、335° | B、255° |
| C、155° | D、150° |
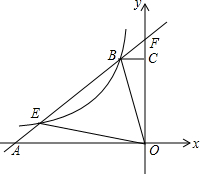 如图,直角梯形OABC的腰OC在y轴的正半轴上,点A(5n,0)在x轴的负半轴上,OA:AB:OC=5:5:3.点D是线段OC上一点,且OD=BD.
如图,直角梯形OABC的腰OC在y轴的正半轴上,点A(5n,0)在x轴的负半轴上,OA:AB:OC=5:5:3.点D是线段OC上一点,且OD=BD. 如图,四边形ABCD是正方形,△ADF通过旋转可得到△ABE,AF=4,AB=8,
如图,四边形ABCD是正方形,△ADF通过旋转可得到△ABE,AF=4,AB=8, 如图,已知∠BOC=4∠AOC,OD平分∠AOB,且∠COD=40°36′,求∠AOB的度数.
如图,已知∠BOC=4∠AOC,OD平分∠AOB,且∠COD=40°36′,求∠AOB的度数. 如图,∠AOB=30°,OP平分∠AOB,PD⊥OB于D,PC∥OB交OA于C,若PC=6,则PD=
如图,∠AOB=30°,OP平分∠AOB,PD⊥OB于D,PC∥OB交OA于C,若PC=6,则PD=