题目内容
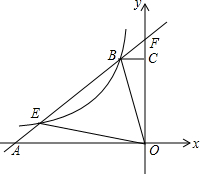 如图,直角梯形OABC的腰OC在y轴的正半轴上,点A(5n,0)在x轴的负半轴上,OA:AB:OC=5:5:3.点D是线段OC上一点,且OD=BD.
如图,直角梯形OABC的腰OC在y轴的正半轴上,点A(5n,0)在x轴的负半轴上,OA:AB:OC=5:5:3.点D是线段OC上一点,且OD=BD.(1)若直线y=kx+m(k≠0)过B、D两点,求k的值;
(2)在(1)的条件下,反比例函数y=
| m |
| x |
①求证:反比例函数y=
| m |
| x |
②设反比例函数y=
| m |
| x |
考点:反比例函数综合题
专题:
分析:(1)根据OA:OC的关系,可得B点的纵坐标,根据勾股定理,可得B点的横坐标,根据OD=BD,可得D点的坐标,根据待定系数法,可得k值;
(2)①根据待定系数法,可得反比例函数解析式,直线AB的解析式,根据代入消元法,可得关于x的一元二次方程,根据一元二次方程根的判别式,可得答案;
②根据解方程组,可得E点坐标,根据点E落在点段PQ上,可得关于n的方程,根据解方程,可得答案.
(2)①根据待定系数法,可得反比例函数解析式,直线AB的解析式,根据代入消元法,可得关于x的一元二次方程,根据一元二次方程根的判别式,可得答案;
②根据解方程组,可得E点坐标,根据点E落在点段PQ上,可得关于n的方程,根据解方程,可得答案.
解答:解:(1)∵A(5n,0),OA:OC=5:3,点C在y轴的正半轴上,
∴C(0,-3n).
∵BC∥OA,
∴B点的纵坐标是-3n,
过点B做BG⊥OA于G点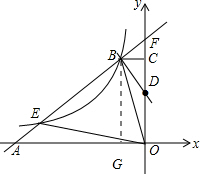 ,
,
则BG=-3n,设OG为x,在Rt△ABG中,由勾股定理,得
(-5n-x)2+(-3n)2=(-5n)2,解得x=-n,x=-9n(不符合题意要舍去),
B(-n,-3n).
设OD=t,点D是线段OC上一点,且OD=BD,
∴t2=(-3n-t)2+(-n)2解得t=-
n,
∴D(0,-
t).
直线y=kx+m(k≠0)过B、D两点,得
,解得k=-
;
(2)①由反比例函数y=
的图象经过点B,得
m═n(-3n)=-3n2,
反比例函数y=-
,
设AB的解析式为y=kx+b,图象经过点A,B,得
,解得
,
AB的解析式为y=
x-
n,
由y=-
和y=
x-
n消去y,并整理得3x2-15nx+12n2=0,
∵△=(-15n)2-4×3×12n2=9n2>0,
∴反比例函数y=
的图象与直线AB必有两个不同的交点;
②联立y=-
和y=
x-
n,得
,解得
,
,
∴E(4n,-
n).
当点E过点P时,-n-1=-
n,解得n=-4;
当点E过点Q时,-n-2=-
n,解得n=-8,
当点E落在点段PQ上时,n的取值范围是-8≤n≤-4.
∴C(0,-3n).
∵BC∥OA,
∴B点的纵坐标是-3n,
过点B做BG⊥OA于G点
 ,
,则BG=-3n,设OG为x,在Rt△ABG中,由勾股定理,得
(-5n-x)2+(-3n)2=(-5n)2,解得x=-n,x=-9n(不符合题意要舍去),
B(-n,-3n).
设OD=t,点D是线段OC上一点,且OD=BD,
∴t2=(-3n-t)2+(-n)2解得t=-
| 5 |
| 3 |
∴D(0,-
| 5 |
| 3 |
直线y=kx+m(k≠0)过B、D两点,得
|
| 4 |
| 3 |
(2)①由反比例函数y=
| m |
| x |
m═n(-3n)=-3n2,
反比例函数y=-
| 3n2 |
| x |
设AB的解析式为y=kx+b,图象经过点A,B,得
|
|
AB的解析式为y=
| 3 |
| 4 |
| 15 |
| 4 |
由y=-
| 3n2 |
| x |
| 3 |
| 4 |
| 15 |
| 4 |
∵△=(-15n)2-4×3×12n2=9n2>0,
∴反比例函数y=
| m |
| x |
②联立y=-
| 3n2 |
| x |
| 3 |
| 4 |
| 15 |
| 4 |
|
|
|
∴E(4n,-
| 3 |
| 4 |
当点E过点P时,-n-1=-
| 3 |
| 4 |
当点E过点Q时,-n-2=-
| 3 |
| 4 |
当点E落在点段PQ上时,n的取值范围是-8≤n≤-4.
点评:本题考查了反比例函数综合题,(1)利用了待定系数法求函数解析式;(2)利用了代入消元法解二元一次方程组,一元二次方程的根的判别式;(3)利用了解方程组,点E经过线段的端点得出不等式组.

练习册系列答案
相关题目
 如图,已知线段AB=a(a>1),线段CD=1,线段CD在线段AB上由点A向点B从左向右移动(点C不与点A重合,点D不与点B重合),若设线段AC=x,记图中所有线段的和为S,则S可表示为( )
如图,已知线段AB=a(a>1),线段CD=1,线段CD在线段AB上由点A向点B从左向右移动(点C不与点A重合,点D不与点B重合),若设线段AC=x,记图中所有线段的和为S,则S可表示为( )| A、3a+1 |
| B、2a+1 |
| C、3a+x-1 |
| D、2a+x+1 |
已知点A,B,C在同一直线上,若AB=20cm,AC=30cm,线段BC的长是( )
| A、10cm |
| B、50cm |
| C、25cm |
| D、10cm或50cm |
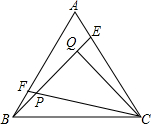 如图,点E,F分别是正△ABC的边AC,AB上的点,AE=BF,BE,CF相交于点P,CQ⊥BE于Q,若PF=1,PQ=3,则BE=
如图,点E,F分别是正△ABC的边AC,AB上的点,AE=BF,BE,CF相交于点P,CQ⊥BE于Q,若PF=1,PQ=3,则BE= 已知如图,点B在线段AC上,AB=8cm,AC=18cm,点P,Q分别是AB,AC的中点,求线段PQ的长.
已知如图,点B在线段AC上,AB=8cm,AC=18cm,点P,Q分别是AB,AC的中点,求线段PQ的长.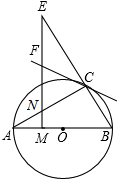 如图,AB是⊙O的直径,且点C为⊙O上的一点,∠BAC=30°,M是OA上一点,过M作AB的垂线交AC于点N,交BC的延长线于点E,直线CF交EN于点F,且∠ECF=∠E.
如图,AB是⊙O的直径,且点C为⊙O上的一点,∠BAC=30°,M是OA上一点,过M作AB的垂线交AC于点N,交BC的延长线于点E,直线CF交EN于点F,且∠ECF=∠E. 反比例函数y=
反比例函数y=
 如图,⊙O是△ABC的外接圆,AB是⊙O的直径,D是AB延长线上一点,AE⊥DC交DC的延长线于点E,且AC平分∠EAB.
如图,⊙O是△ABC的外接圆,AB是⊙O的直径,D是AB延长线上一点,AE⊥DC交DC的延长线于点E,且AC平分∠EAB.