题目内容
13. 如图,已知AM∥BN,∠A=60°.点P是射线AM上一动点(与点A不重合),BC、BD分别平分∠ABP和∠PBN,分别交射线AM于点C,D.
如图,已知AM∥BN,∠A=60°.点P是射线AM上一动点(与点A不重合),BC、BD分别平分∠ABP和∠PBN,分别交射线AM于点C,D.(1)①∠ABN的度数是120°; ②∵AM∥BN,∴∠ACB=∠CBN;
(2)求∠CBD的度数;
(3)当点P运动时,∠APB与∠ADB之间的数量关系是否随之发生变化?若不变化,请写出它们之间的关系,并说明理由;若变化,请写出变化规律.
(4)当点P运动到使∠ACB=∠ABD时,∠ABC的度数是30°.
分析 (1)由平行线的性质:两直线平行同旁内角互补和内错角相等可得;
(2)由(1)知∠ABP+∠PBN=120°,再根据角平分线的定义知∠ABP=2∠CBP、∠PBN=2∠DBP,可得2∠CBP+2∠DBP=120°,即∠CBD=∠CBP+∠DBP=60°;
(3)由AM∥BN得∠APB=∠PBN、∠ADB=∠DBN,根据BD平分∠PBN知∠PBN=2∠DBN,从而可得∠APB:∠ADB=2:1;
(4)由AM∥BN得∠ACB=∠CBN,当∠ACB=∠ABD时有∠CBN=∠ABD,得∠ABC+∠CBD=∠CBD+∠DBN,即∠ABC=∠DBN,根据∠ABN=120°,∠CBD=60°可得答案.
解答 解:(1)①∵AM∥BN,∠A=60°,
∴∠A+∠ABN=180°,
∴∠ABN=120°;
②∵AM∥BN,
∴∠ACB=∠CBN,
故答案为:120°,∠CBN;
(2)∵AM∥BN,
∴∠ABN+∠A=180°,
∴∠ABN=180°-60°=120°,
∴∠ABP+∠PBN=120°,
∵BC平分∠ABP,BD平分∠PBN,
∴∠ABP=2∠CBP,∠PBN=2∠DBP,
∴2∠CBP+2∠DBP=120°,
∴∠CBD=∠CBP+∠DBP=60°;
(3)不变,∠APB:∠ADB=2:1.
∵AM∥BN,
∴∠APB=∠PBN,∠ADB=∠DBN,
∵BD平分∠PBN,
∴∠PBN=2∠DBN,
∴∠APB:∠ADB=2:1;
(4)∵AM∥BN,
∴∠ACB=∠CBN,
当∠ACB=∠ABD时,则有∠CBN=∠ABD,
∴∠ABC+∠CBD=∠CBD+∠DBN,
∴∠ABC=∠DBN,
由(1)可知∠ABN=120°,∠CBD=60°,
∴∠ABC+∠DBN=60°,
∴∠ABC=30°,
故答案为:30°.
点评 本题主要考查平行线的性质和角平分线的定义,熟练掌握平行线的性质是解题的关键.

 阅读快车系列答案
阅读快车系列答案| A. | a2-1 | B. | a2+2a+1 | C. | a2-2a-1 | D. | (1-a)2 |
(1)不妨设该种品牌玩具的销售单价为x元(x>30),请你分别用x的代数式来表示销售量y件和销售该品牌玩具获得利润w元,并把结果填写在表格中:
| 销售单价(元) | x(x>30) |
| 销售量y(件) | -10x+800 |
| 销售玩具获得利润w(元) | -10x2+1000x-16000 |
(3)在第(1)问的条件下,若玩具厂规定该品牌玩具销售单价不低于32元,且商场要完成不少于400件的销售任务,求:商场销售该品牌玩具获得最大利润是多少?
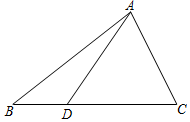 如图,已知点D是△ABC的边BC上一点,且BD=$\frac{1}{2}$CD,设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{BC}$=$\overrightarrow{b}$.
如图,已知点D是△ABC的边BC上一点,且BD=$\frac{1}{2}$CD,设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{BC}$=$\overrightarrow{b}$.