题目内容
19.下列说法中,不正确的是( )| A. | 如果a、b互为相反数,则a+b=0 | B. | a为任意有理数,则它的倒数为$\frac{1}{a}$ | ||
| C. | $\frac{πx{y}^{2}}{7}$的系数是$\frac{π}{7}$ | D. | $\sqrt{81}$的算术平方根是3 |
分析 应用排除法逐项分析即可.
解答 解:A:根据有理数的加法法则:如果两个数互为相反数,那么它们的和为0,故选项A正确;
B:如果a为0,则它的倒数没有意义,故选项B错误;
C:单项式中的数字因数叫做单项式的系数,而π是数而不是字母,故$\frac{π}{7}$是系数,即选项C正确;
D:因为$\sqrt{81}=9$,而9的算术平方根是3,故选项D正确;
故:选B
点评 本题考查了算术平方根、相反数、倒数、单项式,解题的关键是概念要清楚.

练习册系列答案
相关题目
4. 如图,若正六边形ABCDEF绕着中心点O旋转α度后得到的图形与原来图形重合,则α的最小值为( )
如图,若正六边形ABCDEF绕着中心点O旋转α度后得到的图形与原来图形重合,则α的最小值为( )
 如图,若正六边形ABCDEF绕着中心点O旋转α度后得到的图形与原来图形重合,则α的最小值为( )
如图,若正六边形ABCDEF绕着中心点O旋转α度后得到的图形与原来图形重合,则α的最小值为( )| A. | 120° | B. | 90° | C. | 45° | D. | 60° |
11.若|a|=4,|b|=3,且Q(a,b)在第二象限,则a+b的值为( )
| A. | 1 | B. | 7 | C. | -1 | D. | -7 |
8.一水果经销商购进了A,B两种水果各10箱,分配给他的甲、乙两个零售店(分别简称甲店、乙店)销售,预计每箱水果的盈利情况如表:
(1)如果甲、乙两店各配货10箱,其中A种水果两店各5箱,B种水果两店各5箱,请你计算出经销商能盈利多少?
(2)在甲、乙两店各配货10箱(按整箱配送),且保证乙店盈利不少于100元的情况下,请你设计出使水果经销商盈利最大的配货方案.并求出最大盈利为多少?
| A种水果/箱 | B种水果/箱 | |
| 甲店 | 11元 | 17元 |
| 乙店 | 9元 | 13元 |
(2)在甲、乙两店各配货10箱(按整箱配送),且保证乙店盈利不少于100元的情况下,请你设计出使水果经销商盈利最大的配货方案.并求出最大盈利为多少?
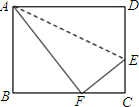 如图,折叠长方形的一边AD,使点D落在BC边上的F点处,若AB=8cm,BC=10cm,则EC长为3cm.
如图,折叠长方形的一边AD,使点D落在BC边上的F点处,若AB=8cm,BC=10cm,则EC长为3cm. 如图,已知Rt△ADE与等腰Rt△ABC有公共顶点A,其中∠E=30°,∠EAC=15°现将△ADE绕着点A逆时针旋转α°(0°<α<180°)得到△AMN.其中直线AM,直线MN分别与直线BC相交于K,L两点,当∠α=15°或60°或330°时.△MKL为等腰三角形.
如图,已知Rt△ADE与等腰Rt△ABC有公共顶点A,其中∠E=30°,∠EAC=15°现将△ADE绕着点A逆时针旋转α°(0°<α<180°)得到△AMN.其中直线AM,直线MN分别与直线BC相交于K,L两点,当∠α=15°或60°或330°时.△MKL为等腰三角形. 如图,已知AB=EF,AD=CE,BC⊥AE,FD⊥AE.求证:
如图,已知AB=EF,AD=CE,BC⊥AE,FD⊥AE.求证: