题目内容
如图，一个牧童在小河南4km的A处牧马，此处在也正位于他的小屋B的西12km北5km处，他想把他的马牵到小河边去饮水，然后回家，他要完成这件事情所走的最短路程是多少？考点：轴对称-最短路线问题
专题：
分析：作出A点关于MN的对称点A′，连接A′B交MN于点P，则A′B就是最短路线；然后构建直角三角形A′BD，利用勾股定理即可求得最短路程．
解答：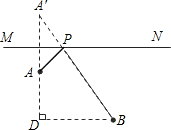
解：如图，作出A点关于MN的对称点A′，连接A′B交MN于点P，
则A′B就是最短路线．
在Rt△A′DB中，由勾股定理求得
A′B=
=
=
km．
答：他要完成这件事情所走的最短路程是
km．
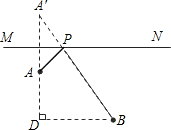解：如图，作出A点关于MN的对称点A′，连接A′B交MN于点P，则A′B就是最短路线．
在Rt△A′DB中，由勾股定理求得
A′B=
| A′D2+DB2 |
| (5+4+4)2+122 |
| 313 |
答：他要完成这件事情所走的最短路程是
| 313 |
点评：本题考查的是勾股定理在实际生活中的运用，需要同学们联系实际，熟练掌握．
练习册系列答案
相关题目
如图，A，B，C三点在同一直线上，△ADC，△BEC是等边三角形，连接AE，BD．求证：函数y=
的自变量x的取值范围是（ ）
| x-4 |
| A、x≠4 | B、x＞4 |
| C、x≥4 | D、x≤4 |
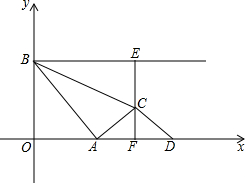如图，点A是x轴正半轴上的动点，点B的坐标为（0，4），将线段AB的中点绕点A按顺时针方向旋转90°得点C，过点C作x轴的垂线，垂足为F，过点B作y轴的垂线与直线CF相交于点E，点D是点A关于直线CF的对称点，连接AC、BC、CD，设点A的横坐标为t．
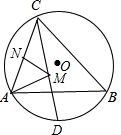如图，△ABC内接于半径为2的⊙O，∠ABC=45°，∠ACB=60°，点D为
在平面直角坐标系xOy中，A（-1，5），B（-1，0），C（-4，3）．