题目内容
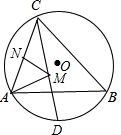 如图,△ABC内接于半径为2的⊙O,∠ABC=45°,∠ACB=60°,点D为
如图,△ABC内接于半径为2的⊙O,∠ABC=45°,∠ACB=60°,点D为 |
| AB |
考点:轴对称-最短路线问题,圆心角、弧、弦的关系,圆周角定理
专题:
分析:连接OA,OC,过点A作AE⊥AC,交CD于点E,过点E作EA′⊥BC于点A′过点A′作A′N′⊥AC于点N′,则A′N′的长即为MA+MN的最小值;先求得AC=2
,然后根据解直角三角形即可求得A′N′=A′C•sin60°=2
×
=
,即MA+MN的最小值是
.
| 2 |
| 2 |
| ||
| 2 |
| 6 |
| 6 |
解答:解:连接OA,OC,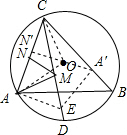
∵∠ABC=45°,OA=OC=2,
∴∠AOC=90°,
∴AC=
=
=2
.
过点A作AE⊥AC,交CD于点E,过点E作EA′⊥BC于点A′过点A′作A′N′⊥AC于点N′,
∵点D为
的中点,
∴CD为∠ACB的平分线,
∴点A与点A′关于直线CD对称,
∴A′N′的长即为MA+MN的最小值,AC=A′C=2
,
∵∠ACB=60°,
∴A′N′=A′C•sin60°=2
×
=
,即MA+MN的最小值是
.

∵∠ABC=45°,OA=OC=2,
∴∠AOC=90°,
∴AC=
| 2OA2 |
| 2×4 |
| 2 |
过点A作AE⊥AC,交CD于点E,过点E作EA′⊥BC于点A′过点A′作A′N′⊥AC于点N′,
∵点D为
 |
| AB |
∴CD为∠ACB的平分线,
∴点A与点A′关于直线CD对称,
∴A′N′的长即为MA+MN的最小值,AC=A′C=2
| 2 |
∵∠ACB=60°,
∴A′N′=A′C•sin60°=2
| 2 |
| ||
| 2 |
| 6 |
| 6 |
点评:本题考查的是轴对称-最短路线问题,根据题意作出辅助线,构造出直角三角形是解答此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
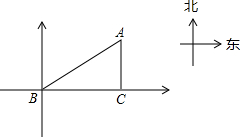 如图,一艘船由西向东航行,上午8时到达B处,看到有一灯塔在它的北偏东60°,距离为72海里的A处,上午10时到达C处,看到灯塔在它的正北方向,则这艘船航行的速度约为( )
如图,一艘船由西向东航行,上午8时到达B处,看到有一灯塔在它的北偏东60°,距离为72海里的A处,上午10时到达C处,看到灯塔在它的正北方向,则这艘船航行的速度约为( )| A、30海里/时 |
| B、31海里/时 |
| C、32海里/时 |
| D、33海里/时 |
 如图,一个牧童在小河南4km的A处牧马,此处在也正位于他的小屋B的西12km北5km处,他想把他的马牵到小河边去饮水,然后回家,他要完成这件事情所走的最短路程是多少?
如图,一个牧童在小河南4km的A处牧马,此处在也正位于他的小屋B的西12km北5km处,他想把他的马牵到小河边去饮水,然后回家,他要完成这件事情所走的最短路程是多少?