题目内容
2.已知(a2-4a+4)+|a-2b|=0,求$\frac{b}{a-b}$•$\frac{{a}^{3}+a{b}^{2}-2{a}^{2}b}{{b}^{3}}$÷$\frac{{a}^{2}-{b}^{2}}{ab+{b}^{2}}$的值.分析 原式利用除法法则变形,约分得到最简结果,利用非负数的性质求出a与b的值,代入原式计算即可得到结果.
解答 解:原式=$\frac{b}{a-b}$•$\frac{a(a-b)^{2}}{{b}^{3}}$•$\frac{b(a+b)}{(a+b)(a-b)}$=$\frac{a}{b}$,
∵(a2-4a+4)+|a-2b|=(a-2)2+|a-2b|=0,
∴a=2,b=1,
则原式=2.
点评 此题考查了分式的化简求值,以及非负数的性质,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
12.在式子:$\frac{2}{n}$,m-3,-13,-$\frac{{m}^{2}}{3}$,2πb2中,单项式有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
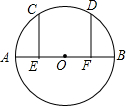 如图,AB是⊙O的直径,点E、F分别是OA、OB的中点,且EC⊥AB,FD⊥AB,EC、FD交⊙O于C、D两点,求证:$\widehat{AC}$=$\widehat{BD}$.
如图,AB是⊙O的直径,点E、F分别是OA、OB的中点,且EC⊥AB,FD⊥AB,EC、FD交⊙O于C、D两点,求证:$\widehat{AC}$=$\widehat{BD}$.