题目内容
7.一个多边形的对角线的条数等于它的边数的4倍,求这个多边形的边数.分析 n边形的对角线有$\frac{1}{2}$n•(n-3)条,根据对角线条数是它边数的5倍列方程即可求得多边形的边数.
解答 解:设这个多边形的边数是n.
根据题意得:$\frac{1}{2}$n•(n-3)=4n,
解得:n=11.
则多边形的边数是11.
点评 本题主要考查了多边形的对角线的条数与多边形的边数之间的关系,解决本题的关键是熟记n边形对角线的公式.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
12.半径为4的圆中,垂直平分一条半径的弦的长是( )
| A. | $\frac{\sqrt{3}}{2}$ | B. | $\sqrt{3}$ | C. | 2$\sqrt{3}$ | D. | 4$\sqrt{3}$ |
17.下列方程一定是一元二次方程的是( )
| A. | (a2+1)x2+bx+c=0 | B. | 5x2-6y-3=0 | C. | ax2-x+2=0 | D. | 3x2+$\frac{2}{x}$-1=0 |
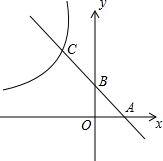 如图,直线y=-2x+1分别交x轴,y轴于点A,B,交反比例函数y=$\frac{k}{x}$的图象于点C,CB:BA=2:1.
如图,直线y=-2x+1分别交x轴,y轴于点A,B,交反比例函数y=$\frac{k}{x}$的图象于点C,CB:BA=2:1.