题目内容
14.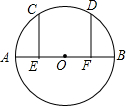 如图,AB是⊙O的直径,点E、F分别是OA、OB的中点,且EC⊥AB,FD⊥AB,EC、FD交⊙O于C、D两点,求证:$\widehat{AC}$=$\widehat{BD}$.
如图,AB是⊙O的直径,点E、F分别是OA、OB的中点,且EC⊥AB,FD⊥AB,EC、FD交⊙O于C、D两点,求证:$\widehat{AC}$=$\widehat{BD}$.
分析 连接OC,OD,根据同圆的半径相等得到OA=OC=OD=OB,由于E、F分别是OA、OB的中点,于是得到OE=OF=$\frac{1}{2}$OA=$\frac{1}{2}$OC=$\frac{1}{2}$OD=$\frac{1}{2}$OB,由EC⊥AB,FD⊥AB,得到∠CEO=∠DFO=90°,根据直角三角形的性质得到∠ECO=∠FDO=30°,于是得到∠AOC=∠DOF=60°,即可得到结论.
解答 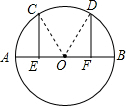 证明:连接OC,OD,
证明:连接OC,OD,
∵OA=OC=OD=OB,
∵E、F分别是OA、OB的中点,
∴OE=OF=$\frac{1}{2}$OA=$\frac{1}{2}$OC=$\frac{1}{2}$OD=$\frac{1}{2}$OB,
∵EC⊥AB,FD⊥AB,
∴∠CEO=∠DFO=90°,
∴∠ECO=∠FDO=30°,
∴∠AOC=∠DOF=60°,
∴$\widehat{AC}$=$\widehat{BD}$.
点评 本题考查了圆心角、弧、弦的关系:在同圆或等圆中,如果两个圆心角、两条弧、两条弦中有一组量相等,那么它们所对应的其余各组量都分别相等.也考查了全等三角形的判定与性质.

练习册系列答案
相关题目
4.学校对七年级女生进行了仰卧起坐的测试,以能做40个为标准,超过的次数用正数表示,不足的次数用负数表示,其中6名女生的成绩如下(单位:个):
(1)这6名女生共做了多少个仰卧起坐?
(2)这6名女生的达标率是多少?(结果精确到百分位)
| 2 | -1 | 0 | 3 | -2 | 1 |
(2)这6名女生的达标率是多少?(结果精确到百分位)
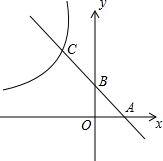 如图,直线y=-2x+1分别交x轴,y轴于点A,B,交反比例函数y=$\frac{k}{x}$的图象于点C,CB:BA=2:1.
如图,直线y=-2x+1分别交x轴,y轴于点A,B,交反比例函数y=$\frac{k}{x}$的图象于点C,CB:BA=2:1.