题目内容
14.已知关于x的一元二次方程x2+2x+2k-2=0有两个不相等的实数根.(1)求k的取值范围;
(2)若k为正整数,求该方程的根.
分析 (1)根据一元二次方程x2+2x+2k-2=0有两个不相等的实数根可得△=22-4(2k-2)=4-8k+8=12-8k>0,求出k的取值范围即可;
(2)根据k的取值范围,结合k为正整数,得到k的值,进而求出方程的根.
解答 解:(1)∵关于x的一元二次方程x2+2x+2k-2=0有两个不相等的实数根,
∴△>0,
∴△=22-4(2k-2)=4-8k+8=12-8k,
∴12-8k>0,
∴k<$\frac{3}{2}$;
(2)∵k<$\frac{3}{2}$,并且k为正整数,
∴k=1,
∴该方程为x2+2x=0,
∴该方程的根为x1=0,x2=-2.
点评 此题考查了一元二次方程ax2+bx+c=0(a≠0)的根的判别式△=b2-4ac:当△>0,方程有两个不相等的实数根;当△=0,方程有两个相等的实数根;当△<0,方程没有实数根.

练习册系列答案
相关题目
2.下列图形中,不是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
6.9的平方根等于( )
| A. | -3 | B. | 3 | C. | ?±3 | D. | $\sqrt{3}$ |
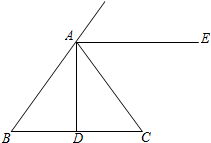 如图,在△ABC中,AB=AC,D为BC边的中点,AE∥BC.
如图,在△ABC中,AB=AC,D为BC边的中点,AE∥BC.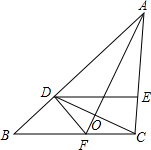 已知:如图,在△ABC中,D是AB上一点,且AD=AC,∠DAO=∠CAO,DE∥BC.求证:CD平分∠EDF.
已知:如图,在△ABC中,D是AB上一点,且AD=AC,∠DAO=∠CAO,DE∥BC.求证:CD平分∠EDF.