Question

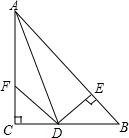
如图，△ABC中，BD平分∠ABC，BC的中垂线交BC于点E，交BD于点F，连接CF．若∠A=60°，∠ABD=24°，则∠ACF的度数为(     )

A．48°   B．36°    C．30°   D．24°

Answer 1

A【考点】线段垂直平分线的性质．

【分析】根据角平分线的性质可得∠DBC=∠ABD=24°，然后再计算出∠ACB的度数，再根据线段垂直平分线的性质可得BF=CF，进而可得∠FCB=24°，然后可算出∠ACF的度数．

【解答】解：∵BD平分∠ABC，

∴∠DBC=∠ABD=24°，

∵∠A=60°，

∴∠ACB=180°﹣60°﹣24°×2=72°，

∵BC的中垂线交BC于点E，

∴BF=CF，

∴∠FCB=24°，

∴∠ACF=72°﹣24°=48°，

故选：A．

【点评】此题主要考查了线段垂直平分线的性质，以及三角形内角和定理，关键是掌握线段垂直平分线上任意一点，到线段两端点的距离相等．