题目内容
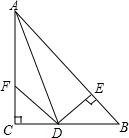
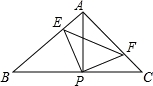
如图:在△ABC中,∠C=90°,AD是∠BAC的平分线,DE⊥AB于E,F在AC上,BD=DF;
求证:(1)CF=EB;
(2)AB=AC+CF.
【考点】全等三角形的判定与性质;角平分线的性质.
【专题】证明题.
【分析】(1)根据角平分线的性质“角的平分线上的点到角的两边的距离相等”,可得点D到AB的距离=点D到AC的距离即CD=DE.再根据Rt△CDF≌Rt△EBD,得CF=EB;
(2)利用角平分线性质证明∴△ADC≌△ADE,AC=AE,再将线段AC进行转化.
【解答】解:(1)∵AD是∠BAC的平分线,DE⊥AB,DC⊥AC,
∴DE=DC,
在Rt△DCF和Rt△DEB中,
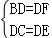 ,
,
∴Rt△CDF≌Rt△EBD(HL),
∴CF=EB;
(2)在△ADC与△ADE中,
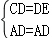 ,
,
∴△ADC≌△ADE(HL),
∴AC=AE,
∴AB=AE+BE=AC+CF.
【点评】本题主要考查平分线的性质,全等三角形的性质与判定,由已知能够注意到点D到AB的距离=点D到AC的距离,即CD=DE,是解答本题的关键.

在创建国家卫生城市环境综合整治行动中,某小区计划对楼体外墙进行粉刷,现有甲、乙两家装饰公司有意承接此项工程.已知甲公司的费用y(元)与粉刷面积x(x≥100)(m2)的关系如表:
| 粉刷面积x(m2) | 100 | 200 | 300 | 400 | … |
| 费用y(元) | 2000 | 4000 | 6000 | 8000 | … |
乙公司表示:若该小区先支付3000元的基本承包费,则可按15元/m2的价格收费.请根据以上信息,解答下列问题:
(1)若甲公司收取的费用y(元)与粉刷面积x(m2)满足我们学过某一函数关系,试确定这一函数关系式;
(2)试确定乙公司收取的费用y(元)与粉刷面积x(x≥100)(m2)满足的函数关系式;
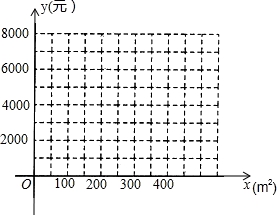
(3)在给出的平面直角坐标系内画出(1)(2)中的函数图象,并确定若该小区粉刷面积约为800m2,则选择哪家装饰公司进行施工更合算?
 ,其中x=2﹣2,y=﹣2015.
,其中x=2﹣2,y=﹣2015.

 的点表示的数是__________.
的点表示的数是__________. 的结果是(
的结果是( )
) B.
B. C.
C. D.
D.