题目内容
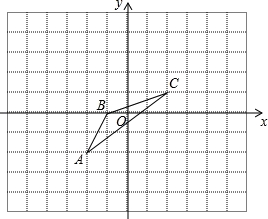
已知:如图,CD⊥AB,BE⊥AC,垂足分别为D、E,BE、CD相交于O点,∠1=∠2.图中全等的三角形共有( )

A.4对 B.3对 C.2对 D.1对
A【考点】全等三角形的判定.
【分析】解此题的关键是三角形全等的判定定理的准确应用.三角形全等的判定定理有:SSS,SAS,ASA,AAS.做题时要从已知入手由易到难,不重不漏.
【解答】解:∵CD⊥AB,BE⊥AC,
∴∠ADO=∠AEO=90°;
∵∠1=∠2,AO=AO,
∴△ADO≌△AEO(AAS).
∴AD=AE,
∵∠DAC=∠EAB,∠ADO=∠AEO,
∴△ADC≌△AEB(ASA).
∴AB=AC,
∵∠1=∠2,AO=AO,
∴△AOB≌△AOC(SAS).
∴∠B=∠C,
∵AD=AE,AB=AC,
∴DB=EC;
∵∠BOD=∠COE,
∴△BOD≌△COE(AAS).
故选A.
【点评】此题考查了三角形全等的判定与性质,解题的关键是要注意正确识图.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案在创建国家卫生城市环境综合整治行动中,某小区计划对楼体外墙进行粉刷,现有甲、乙两家装饰公司有意承接此项工程.已知甲公司的费用y(元)与粉刷面积x(x≥100)(m2)的关系如表:
| 粉刷面积x(m2) | 100 | 200 | 300 | 400 | … |
| 费用y(元) | 2000 | 4000 | 6000 | 8000 | … |
乙公司表示:若该小区先支付3000元的基本承包费,则可按15元/m2的价格收费.请根据以上信息,解答下列问题:
(1)若甲公司收取的费用y(元)与粉刷面积x(m2)满足我们学过某一函数关系,试确定这一函数关系式;
(2)试确定乙公司收取的费用y(元)与粉刷面积x(x≥100)(m2)满足的函数关系式;
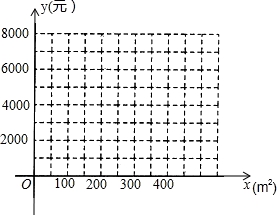
(3)在给出的平面直角坐标系内画出(1)(2)中的函数图象,并确定若该小区粉刷面积约为800m2,则选择哪家装饰公司进行施工更合算?


 =﹣
=﹣ B.
B. C.
C. =﹣
=﹣ =﹣
=﹣
 的结果是(
的结果是( )
) B.
B. C.
C. D.
D.
 平面直角坐标系中,
平面直角坐标系中,