题目内容
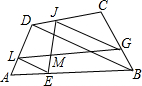如图，在四边形ABCD的各边上取点E、G，J，L，已知| AE |
| AB |
| DJ |
| DC |
| 1 |
| 3 |
| AL |
| AD |
| BG |
| BC |
| 1 |
| 3 |
| LM |
| LG |
| 1 |
| 3 |
考点：平行线分线段成比例
专题：证明题
分析：由已知的两比例式，得到
=
=
，
=
=
，可得出LE与BD平行，JG与BD平行，利用平行于同一条直线的两直线平行得到LE与JG平行，同时得到LE与JG的比值，再由LE与JG平行，得到三角形LEM与三角形GJM相似，由相似得比例得到LM与MG的比值为1：2，利用比例的性质即可求出LM与LG的比值为1：3，得证．
| AE |
| AB |
| AL |
| AD |
| 1 |
| 3 |
| DJ |
| DC |
| BG |
| BC |
| 1 |
| 3 |
解答：证明：∵
=
=
，
=
=
，
∴
=
=
，
=
=
，
∴LE∥DB，JG∥DB，
∴
=
，
=
=
=
，LE∥JG，
∴
=
，且△LEM∽△GJM，
∴
=
=
，
则
=
=
．
| AE |
| AB |
| DJ |
| DC |
| 1 |
| 3 |
| AL |
| AD |
| BG |
| BC |
| 1 |
| 3 |
∴
| AE |
| AB |
| AL |
| AD |
| 1 |
| 3 |
| DJ |
| DC |
| BG |
| BC |
| 1 |
| 3 |
∴LE∥DB，JG∥DB，
∴
| LE |
| DB |
| 1 |
| 3 |
| JG |
| DB |
| JC |
| DC |
| DC-DJ |
| DC |
| 2 |
| 3 |
∴
| LE |
| JG |
| 1 |
| 2 |
∴
| LM |
| MG |
| LE |
| JG |
| 1 |
| 2 |
则
| LM |
| LG |
| LM |
| LM+MG |
| 1 |
| 3 |
点评：此题考查了平行线分线段成比例，比例的性质，以及相似三角形的判定与性质，熟练掌握性质是解本题的关键．
练习册系列答案
相关题目
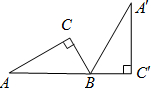如图，Rt△A′BC′是由Rt△ABC绕B点顺时针旋转而得，且点A，B，C′在同一条直线上，在Rt△ABC中，若∠C=90°，BC=2，AB=4，求斜边AB旋转到A′B所扫过的扇形面积．