题目内容
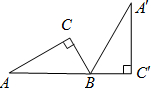 如图,Rt△A′BC′是由Rt△ABC绕B点顺时针旋转而得,且点A,B,C′在同一条直线上,在Rt△ABC中,若∠C=90°,BC=2,AB=4,求斜边AB旋转到A′B所扫过的扇形面积.
如图,Rt△A′BC′是由Rt△ABC绕B点顺时针旋转而得,且点A,B,C′在同一条直线上,在Rt△ABC中,若∠C=90°,BC=2,AB=4,求斜边AB旋转到A′B所扫过的扇形面积.考点:扇形面积的计算,旋转的性质
专题:计算题
分析:根据直角三角形的性质可知∠A=30°,∠ABC=60°,根据旋转的性质得∠A′BC′=60°,则∠ABA′=120°,从而根据扇形面积公式S=
进行计算.
| nπr2 |
| 360 |
解答:解:∵∠C=90°,BC=2,AB=4,
∴∠A=30°.
∴∠ABC=60°.
根据旋转的性质,得∠A′BC′=∠ABC=60°.
则∠ABA′=120°.
∴S=
=
=
.
故斜边AB旋转到A′B所扫过的扇形面积为
.
∴∠A=30°.
∴∠ABC=60°.
根据旋转的性质,得∠A′BC′=∠ABC=60°.
则∠ABA′=120°.
∴S=
| nπr2 |
| 360 |
| 120π×16 |
| 360 |
| 16π |
| 3 |
故斜边AB旋转到A′B所扫过的扇形面积为
| 16π |
| 3 |
点评:本题考查扇形面积的计算,要求掌握扇形的面积公式:(1)利用圆心角和半径:S=
;(2)利用弧长和半径:S=
lr,学会针对不同的题型选择合适的方法.
| nπr2 |
| 360 |
| 1 |
| 2 |

练习册系列答案
相关题目
我市最大规模的民生工程--北改工程于2012年2月正式拉开大幕.据初步统计,整个工程项目约360个,总投资约为3300亿元.将总投资用科学记数法表示应约为( )
| A、3.3×109元 |
| B、3.3×1010元 |
| C、3.3×1011元 |
| D、3.3×1012元 |
 解不等式
解不等式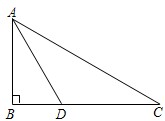 如图,某中学九年级数学兴趣小组测量校内旗杆AB高度,在C点测得旗杆顶端A的仰角为30°,向前走了26米到达D点,在D点测得旗杆顶端A的仰角为60°(测角器的高度忽略不计,点B、D、C在同一直线上),求旗杆AB的高度(结果保留3个有效数字,
如图,某中学九年级数学兴趣小组测量校内旗杆AB高度,在C点测得旗杆顶端A的仰角为30°,向前走了26米到达D点,在D点测得旗杆顶端A的仰角为60°(测角器的高度忽略不计,点B、D、C在同一直线上),求旗杆AB的高度(结果保留3个有效数字,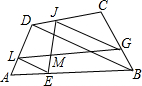 如图,在四边形ABCD的各边上取点E、G,J,L,已知
如图,在四边形ABCD的各边上取点E、G,J,L,已知