题目内容
现将背面完全相同，正面分别标有数1、0、-2、-3的4张卡片洗匀后，背面朝上，从中任取一张，将该卡片上的数记为m，将卡片放回，混合均匀后再从中任取一张，将该卡片上的数记为n，则数字m，n使得关于x的一元一次不等式mx+3n＞2的解一定大于2的概率是 ．
考点：列表法与树状图法,解一元一次不等式
专题：计算题
分析：根据题意列出表格，得到所有可能的情况有16种情况，将m与n的值代入不等式mx+3n＞2中检验，得到解大于2时m与n的值有3种情况，进而求出数字m，n使得关于x的一元一次不等式mx+3n＞2的解一定大于2的概率．
解答：解：根据题意列表如下：
得到所有的情况有16个，其中满足等式mx+3n＞2的解大于2的有：（1，0），（1，-2），（1，-3）共3个，
则数字m，n使得关于x的一元一次不等式mx+3n＞2的解一定大于2的概率P=
．
故答案为：
．
| 1 | 0 | -2 | -3 | |
| 1 | （1，1） | （0，1） | （-2，1） | （-3，1） |
| 0 | （1，0） | （0，0） | （-2，0） | （-3，0） |
| -2 | （1，-2） | （0，-2） | （-2，-2） | （-3，-2） |
| -3 | （1，-3） | （0，-3） | （-2，-3） | （-3，-3） |
则数字m，n使得关于x的一元一次不等式mx+3n＞2的解一定大于2的概率P=
| 3 |
| 16 |
故答案为：
| 3 |
| 16 |
点评：此题考查了利用列表法与树状图法求事件的概率，以及一元一次不等式的解法，其中概率=所求情况数与总情况数之比．
练习册系列答案
相关题目
已知二次函数y=ax2+bx+c（a≠0）的图象如图所示，下列结论中正确的结论是（ ）| A、abc＞0 |
| B、a+b＞m（am+b），（m为实数且m≠1） |
| C、b＜a+c |
| D、2a-b=0 |
如图，直线y=-2x+6与坐标轴相交于点A、点B，BC⊥AB，且
解不等式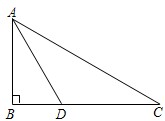
如图，某中学九年级数学兴趣小组测量校内旗杆AB高度，在C点测得旗杆顶端A的仰角为30°，向前走了26米到达D点，在D点测得旗杆顶端A的仰角为60°（测角器的高度忽略不计，点B、D、C在同一直线上），求旗杆AB的高度（结果保留3个有效数字，我市最大规模的民生工程--北改工程于2012年2月正式拉开大幕．据初步统计，整个工程项目约360个，总投资约为3300亿元．将总投资用科学记数法表示应约为（ ）
| A、3.3×109元 |
| B、3.3×1010元 |
| C、3.3×1011元 |
| D、3.3×1012元 |
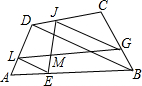如图，在四边形ABCD的各边上取点E、G，J，L，已知