题目内容
13.已知多项式x3-mx2+nx+10有因式x-2和x+1,求m的值.分析 由x3-mx2+nx+10有因式x-2和x+1得到x=2、x=-1肯定是关于x的方程x3-mx2+nx+10=0的两个根,所以将其分别代入该方程列出关于m、n的方程组,通过解方程组来求m、n的值.
解答 解:∵多项式x3-mx2+nx+10有因式x-2和x+1,
∴x=2、x=-1肯定是关于x的方程x3-mx2+nx+10=0的两个根,则
$\left\{\begin{array}{l}{8-4m+2n+10=0}\\{-1-m-n+10=0}\end{array}\right.$,即$\left\{\begin{array}{l}{-4m+2n=-18}\\{-m-n=-9}\end{array}\right.$,
解得$\left\{\begin{array}{l}{m=6}\\{n=3}\end{array}\right.$.
故m的值为6.
点评 本题考查了因式分解的意义,根据因式分解的意义得到x=2、x=-1肯定是关于x的方程x3-mx2+nx+10=0的两个根是解题的难点.

练习册系列答案
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案
相关题目
18.下列运算正确的是( )
| A. | 3m4÷m3=3m2 | B. | m+m2=m3 | C. | (m+n)(m-n)=m2-n2 | D. | ($\frac{m}{2}$)3=$\frac{{m}^{3}}{2}$ |
2.直线l的解析式是y=kx+2,其中k是不等式组$\left\{\begin{array}{l}{3k+4<0}\\{k+9<0}\end{array}\right.$的解,则直线l的图象不经过( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
3.将235000000用科学记数法表示为( )
| A. | 235×106 | B. | 2.35×107 | C. | 2.35×108 | D. | 2.35×109 |
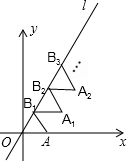 如图放置的△OAB1,△B1A1B2,△B2A2B3,…都是边长为1的等边三角形,点A在x轴上,点O,B1,B2,B3,…都在直线l上,则点A2016的坐标是(1009,1008$\sqrt{3}$).
如图放置的△OAB1,△B1A1B2,△B2A2B3,…都是边长为1的等边三角形,点A在x轴上,点O,B1,B2,B3,…都在直线l上,则点A2016的坐标是(1009,1008$\sqrt{3}$). 如图,在半径为4cm的⊙O中,劣弧AB的长为2πcm,则∠C=45度.
如图,在半径为4cm的⊙O中,劣弧AB的长为2πcm,则∠C=45度.