题目内容
 如图,在?ABCD中,E是BC的中点,且∠AEC=∠DCE,则下列结论正确的有( )
如图,在?ABCD中,E是BC的中点,且∠AEC=∠DCE,则下列结论正确的有( )①S△AFD=2S△EFB;②BF=
| 1 |
| 2 |
| A、1个 | B、2个 | C、3个 | D、4个 |
考点:平行四边形的性质,等腰梯形的判定
专题:
分析:根据已知条件即可推出△BEF∽△DAF,推出②为正确,已知条件可以推出四边形AECD为等腰梯形,推出③正确,结合平行四边形的性质,可以推出④正确,所以①错误的.
解答:解:∵AD∥BC,
∴△AFD∽△EFB,
∴
=
=
=
,
故S△AFD=4S△EFB;故①错误,②正确;
由∠AEC=∠DCE可得∠EAD=∠CDA,∴四边形AECD是等腰梯形,故③正确;
∵∠DAE=∠AEB,∠EAD=∠ADC,
∴④∠AEB=∠ADC正确.
故选:C.
∴△AFD∽△EFB,
∴
| BF |
| DF |
| BE |
| AD |
| EF |
| AF |
| 1 |
| 2 |
故S△AFD=4S△EFB;故①错误,②正确;
由∠AEC=∠DCE可得∠EAD=∠CDA,∴四边形AECD是等腰梯形,故③正确;
∵∠DAE=∠AEB,∠EAD=∠ADC,
∴④∠AEB=∠ADC正确.
故选:C.
点评:此题主要考查了平行四边形的性质以及等腰梯形的判定和相似三角形的性质与判定等知识,解决本题的关键是利用相似求得各对应线段的比例关系.

练习册系列答案
相关题目
已知圆锥的底面半径为5cm,母线长为16cm,则圆锥的侧面积是( )
| A、40πcm2 |
| B、80πcm2 |
| C、40cm2 |
| D、80cm2 |
已知二次函数y=(a-1)x2-2x+1的图象与x轴有两个交点,则a的取值范围是( )
| A、a<2 | B、a>2 |
| C、a<2且a≠1 | D、a<-2 |
把抛物线y=ax2+c向上平移2个单位,得到抛物线y=x2,则a、c的值分别是( )
| A、1、2 | B、1、-2 |
| C、-1、2 | D、-1、-2 |
在△ABC中,AD是的角平分线,自D向AB、AC两边作垂线,垂足为E、F,则下列结论错误的是( )
| A、DE=DF |
| B、AE=AF |
| C、BD=CD |
| D、∠ADE=∠ADF |
 如图,DE是AC的垂直平分线,AE=9cm,△ABD的周长为39cm,那么△ABC的周长为( )
如图,DE是AC的垂直平分线,AE=9cm,△ABD的周长为39cm,那么△ABC的周长为( )| A、39cm | B、48cm |
| C、57cm | D、21cm |
 我们定义:若一条直线能将一矩形的周长和面积同时平分,则这条直线叫做这个矩形的一条和谐直线.如图矩形ABCD中,已知AB=8,AD=10,并设点B的坐标为(m,0),其中m>0.CE=3,若点G(5,8)在过点E的和谐直线上,则m的值为=
我们定义:若一条直线能将一矩形的周长和面积同时平分,则这条直线叫做这个矩形的一条和谐直线.如图矩形ABCD中,已知AB=8,AD=10,并设点B的坐标为(m,0),其中m>0.CE=3,若点G(5,8)在过点E的和谐直线上,则m的值为=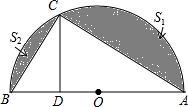 如图,AB是半圆的直径,C是半圆弧上一点,CD⊥AB于D,
如图,AB是半圆的直径,C是半圆弧上一点,CD⊥AB于D,