题目内容
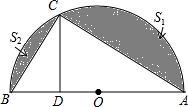 如图,AB是半圆的直径,C是半圆弧上一点,CD⊥AB于D,
如图,AB是半圆的直径,C是半圆弧上一点,CD⊥AB于D,(1)若tan∠BCD=
| 1 |
| 2 |
(2)若AB=8,BD=2,设两弓形的面积(图中阴影部分)为S1和S2,求S1-S2.
考点:扇形面积的计算,圆周角定理
专题:
分析:(1)根据等角的三角函数值相等和勾股定理求出BD的长,再根据勾股定理求出CD的长;
(2)根据扇形的面积公式求出S1和S2,再相减即可.
(2)根据扇形的面积公式求出S1和S2,再相减即可.
解答:解:(1)∵∠B+∠CAD=90°,∠B+∠BCD=90°,
∴∠CAD=∠BCD,
∴tan∠CAB=tan∠BCD=
,
∴AC=2BC,
∴BC2+(2BC)2=AB2,
∴BC2+(2BC)2=100,
∴BC2=20,
∵BD=
CD,
∴BD2+CD2=BC2,
∴(
CD)2+CD2=102,
∴CD=4
.
(2)方法一:∵OA=OB,
∴△AOC与△BOC的面积相等,
∴S1-S2=
×π×42-
×π×42=
π-
π=
π;
方法二:S1=
×π×42-
×4×2
=
π-4
,
S2=
×π×42-
×4×2
=
π-4
,
∴S1-S2=
π-
π=
π.
∴∠CAD=∠BCD,
∴tan∠CAB=tan∠BCD=
| 1 |
| 2 |
∴AC=2BC,
∴BC2+(2BC)2=AB2,
∴BC2+(2BC)2=100,
∴BC2=20,
∵BD=
| 1 |
| 2 |
∴BD2+CD2=BC2,
∴(
| 1 |
| 2 |
∴CD=4
| 5 |
(2)方法一:∵OA=OB,
∴△AOC与△BOC的面积相等,
∴S1-S2=
| 120 |
| 360 |
| 60 |
| 360 |
| 16 |
| 3 |
| 8 |
| 3 |
| 8 |
| 3 |
方法二:S1=
| 120 |
| 360 |
| 1 |
| 2 |
| 3 |
| 16 |
| 3 |
| 3 |
S2=
| 60 |
| 360 |
| 1 |
| 2 |
| 3 |
| 8 |
| 3 |
| 3 |
∴S1-S2=
| 16 |
| 3 |
| 8 |
| 3 |
| 8 |
| 3 |
点评:本题考查了扇形面积的计算,根据图形特点,找到公式适用的条件是解题的关键.

练习册系列答案
相关题目
 如图,在?ABCD中,E是BC的中点,且∠AEC=∠DCE,则下列结论正确的有( )
如图,在?ABCD中,E是BC的中点,且∠AEC=∠DCE,则下列结论正确的有( ) 尺规作图(不写作法,仅保留作图痕迹,在原图上不给分):
尺规作图(不写作法,仅保留作图痕迹,在原图上不给分):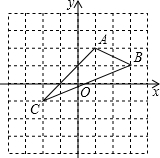 如图,在平面直角坐标系中,A(1,2),B(3,1),C(-2,-1).
如图,在平面直角坐标系中,A(1,2),B(3,1),C(-2,-1). 在正方形网格中,每个小正方形的顶点称为格点,以格点连线为边的三角形叫做格点三角形,如图1、图2中的△ABC和△DEF都是格点三角形.
在正方形网格中,每个小正方形的顶点称为格点,以格点连线为边的三角形叫做格点三角形,如图1、图2中的△ABC和△DEF都是格点三角形.