题目内容
15.某超市销售甲.乙两种商品,甲商品每件进价10元,售价15元,乙商品每件进价30元,售价40元.(1)若该超市同时一次购进两种商品共80件,且恰好用去1600元,求能购进甲、乙两种商品各多少件?
(2)该超市要使两种商品共80件的购进费用不超过1640元,且总利润(利润=售价-进价)不少于600元,你帮助该超市设计相应的进货方案.并指出该超市利润最大的方案.
分析 (1)设该超市购进甲商品x件,则购进乙商品(80-x)件,根据恰好用去1600元,求出x的值,即可得到结果;
(2)设该超市购进甲商品x件,乙商品(80-x)件,根据两种商品共80件的购进费用不超过1640元,且总利润(利润=售价-进价)不少于600元列出不等式组,求出不等式组的解集确定出x的值,即可设计相应的进货方案,并找出使该超市利润最大的方案.
解答 解:(1)设该超市购进甲商品x件,则购进乙商品(80-x)件,
根据题意得:10x+30(80-x)=1600,
解得:x=40,
80-x=40,
则购进甲种商品40件、乙种商品40件;
(2)设该超市购进甲商品x件,乙商品(80-x)件,
由题意得:$\left\{\begin{array}{l}{10x+30(80-x)≤1640}\\{5x+10(80-x)≥600}\end{array}\right.$,
解得:38≤x≤40,
∵x为非负整数,
∴x=38,39,40,相应地y=42,41,40,
进而利润分别为:
5×38+10×42=190+420=610(元),
5×39+10×41=195+410=605(元),
5×40+10×40=200+400=600(元),
则该超市利润最大的方案是购进甲商品38件,乙商品42件.
点评 此题考查了一元一次不等式组的应用,以及一元一次方程的应用,找出题中的等量关系及不等式关系是解本题的关键.

练习册系列答案
相关题目
6.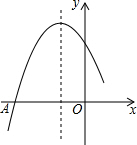 如图是二次函数y=ax2+bx+c图象的一部分,图象过点A(-3,0),对称轴为直线x=-1,给出四个结论,其中正确结论是( )
如图是二次函数y=ax2+bx+c图象的一部分,图象过点A(-3,0),对称轴为直线x=-1,给出四个结论,其中正确结论是( )
 如图是二次函数y=ax2+bx+c图象的一部分,图象过点A(-3,0),对称轴为直线x=-1,给出四个结论,其中正确结论是( )
如图是二次函数y=ax2+bx+c图象的一部分,图象过点A(-3,0),对称轴为直线x=-1,给出四个结论,其中正确结论是( )| A. | b2<4ac | |
| B. | 2a+b=0 | |
| C. | a+b+c>0 | |
| D. | 若点B($\frac{5}{2}$,y1)、C($\frac{1}{2}$,y2)为函数图象上的两点,则y1<y2 |
4.小明本学期的数学测验成绩如表所示:
(1)求六次测验成绩的众数和中位数;
(2)求小明本学期的数学平时测验的平均成绩;
(3)如果本学期的总评成绩是将平时测验的平均成绩、期中测验成绩、期末测验成绩按照3:3:4的比例计算所得,计算小明本学期学科的总评成绩.
| 测验 类别 | 平时测验 | 期中 测验 | 期末 测验 | |||
| 第1次 | 第2此 | 第3次 | 第4次 | |||
| 成绩 | 80 | 86 | 84 | 90 | 90 | 95 |
(2)求小明本学期的数学平时测验的平均成绩;
(3)如果本学期的总评成绩是将平时测验的平均成绩、期中测验成绩、期末测验成绩按照3:3:4的比例计算所得,计算小明本学期学科的总评成绩.
5.若点P(3-m,m-1)在第二象限,则m的取值范围是( )
| A. | m>3 | B. | m<1 | C. | m>1 | D. | 1<m<3 |
 如图,已知抛物线l1经过原点与A点,其顶点是P(-2,3),平行于y轴的直线m与x轴交于点B(b,0),与抛物线l1交于点M.
如图,已知抛物线l1经过原点与A点,其顶点是P(-2,3),平行于y轴的直线m与x轴交于点B(b,0),与抛物线l1交于点M.