题目内容
1.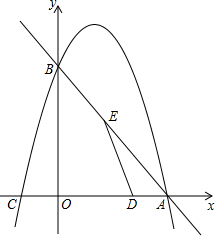 如图,在平面直角坐标系中,直线$y=-\frac{4}{3}x+8$与x轴,y轴分别交于点A、B,抛物线y=ax2-4ax+c经过点A和点B,与x轴的另一个交点为C,动点D从点A出发,以每秒1个单位长度的速度向O点运动,同时动点E从点B出发,以每秒2个单位长度的速度向A点运动,设运动的时间为t秒,0<t<5.
如图,在平面直角坐标系中,直线$y=-\frac{4}{3}x+8$与x轴,y轴分别交于点A、B,抛物线y=ax2-4ax+c经过点A和点B,与x轴的另一个交点为C,动点D从点A出发,以每秒1个单位长度的速度向O点运动,同时动点E从点B出发,以每秒2个单位长度的速度向A点运动,设运动的时间为t秒,0<t<5.(1)求抛物线的解析式;
(2)当t为何值时,以A、D、E为顶点的三角形与△AOB相似;
(3)当△ADE为等腰三角形时,求t的值;
(4)抛物线上是否存在一点F,使得以A、B、D、F为顶点的四边形是平行四边形?若存在,直接写出F点的坐标;若不存在,说明理由.
分析 (1)利用待定系数法即可得出结论;
(2)先表示出AD=t,AE=10-2t,分两种情况,用得出的比例式建立方程求解即可;
(3)先表示出AD=t,AE=10-2t,分三种情况,用两腰相等建立方程求解即可;
(4)分AD为平行四边形的对角线和边两种情况建立方程求解即可.
解答 解:(1)∵A(6,0),B(0,8),依题意知$\left\{\begin{array}{l}36a-24a+c=0\\ c=8\end{array}\right.$,
解得$\left\{\begin{array}{l}a=-\frac{2}{3}\\ c=8\end{array}\right.$,
∴$y=-\frac{2}{3}{x^2}+\frac{8}{3}x+8$.
(2)∵A(6,0),B(0,8),
∴OA=6,OB=8,AB=10,
∴AD=t,AE=10-2t,
①当△ADE∽△AOB时,$\frac{AD}{AO}=\frac{AE}{AB}$,
∴$\frac{t}{6}=\frac{10-2t}{10}$,
∴$t=\frac{30}{11}$;
②当△AED∽△AOB时,$\frac{AE}{AO}=\frac{AD}{AB}$,
∴$\frac{10-2t}{6}=\frac{t}{10}$,
∴$t=\frac{50}{13}$;
综上所述,t的值为$\frac{30}{11}$或$\frac{50}{13}$.
(3)由(2)知,AD=t,AE=10-2t,
①当AD=AE时,
∴t=10-2t,
∴$t=\frac{10}{3}$;
②当AE=DE时,
如图1,过E作EH⊥x轴于点H,
则AD=2AH,
由△AEH∽△ABO得,AH=$\frac{3(10-2t)}{5}$,
∴$t=\frac{6(10-2t)}{5}$,
∴$t=\frac{60}{17}$;
③当AD=DE时,
如图2, 过D作DM⊥AB于点M,
过D作DM⊥AB于点M,
则AE=2AM,
由△AMD∽△AOB得,AM=$\frac{3t}{5}$,
∴$10-2t=\frac{6t}{5}$,
∴$t=\frac{25}{8}$;
综上所述,t的值为$\frac{10}{3}$或$\frac{60}{17}$或$\frac{25}{8}$.
(4)①当AD为边时,则BF∥x轴,
∴yF=yB=8,
∴x=4,
∴F(4,8);
②当AD为对角线时,则yF=-yB=-8,
∴$-\frac{2}{3}{x^2}+\frac{8}{3}x+8=-8$,解得$x=2±2\sqrt{7}$,
∵x>0,
∴$x=2+2\sqrt{7}$,
∴$(2+2\sqrt{7},-8)$.
综上所述,符合条件的点F存在,共有两个F1(4,8),${F_2}(2+2\sqrt{7}$,-8).
点评 此题是二次函数综合题,主要考查了待定系数法,相似三角形的判定和性质,等腰三角形的性质,平行四边形的性质,用方程的思想是解决此类问题的关键,是一道中等难度的中考常考题.

 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案| A. | 2 | B. | 3 | C. | -2 | D. | 8 |
| A. | 3 | B. | -1 | C. | 3或-1 | D. | -3或1 |
 如图是某个几何体的三视图,该几何体是( )
如图是某个几何体的三视图,该几何体是( )| A. | 棱柱 | B. | 圆锥 | C. | 球 | D. | 圆柱 |
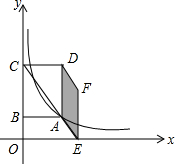 如图所示,在平面直角坐标系中,矩形ABCD的BC边落在y轴上,其它部分均在第一象限,双曲线y=$\frac{k}{x}$过点A,延长对角线CA交x轴于点E,以AD、AE为边作平行四边形AEFD,若平行四边形AEFD的面积为4,则k值为( )
如图所示,在平面直角坐标系中,矩形ABCD的BC边落在y轴上,其它部分均在第一象限,双曲线y=$\frac{k}{x}$过点A,延长对角线CA交x轴于点E,以AD、AE为边作平行四边形AEFD,若平行四边形AEFD的面积为4,则k值为( )

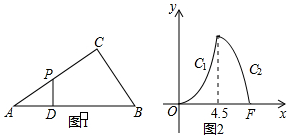 如图1,在Rt△ABC中,∠C=Rt∠,∠A=30°,D为AB上一个动点,过点D作DP⊥AB交折线A-C-B于点P,设AD的长为x,△APD的面积为y,y关于x的函数图象由C1,C2两段组成,如图2所示.
如图1,在Rt△ABC中,∠C=Rt∠,∠A=30°,D为AB上一个动点,过点D作DP⊥AB交折线A-C-B于点P,设AD的长为x,△APD的面积为y,y关于x的函数图象由C1,C2两段组成,如图2所示.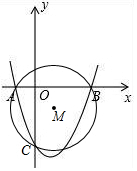 如图,抛物线y=x2-2x-3与x轴交于A(-1,0),B(3,0)两点,与y轴交于点C.⊙M过A、B、C三点,P是抛物线上一点,连接PA,当PA与⊙M相切时,求点P的坐标.
如图,抛物线y=x2-2x-3与x轴交于A(-1,0),B(3,0)两点,与y轴交于点C.⊙M过A、B、C三点,P是抛物线上一点,连接PA,当PA与⊙M相切时,求点P的坐标.