题目内容
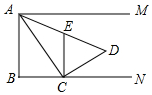
12.已知在Rt△BAC中,∠BAC=90°,AB=AC,点D为射线BC上一点(与点B不重合),过点C作CE⊥BC于点C,且CE=BD(点E与点A在射线BC同侧),连接AD,ED.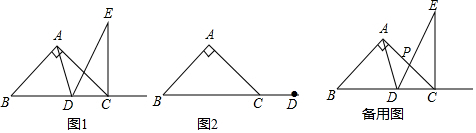
(1)如图1,当点D在线段BC上时,请直接写出∠ADE的度数.
(2)当点D在线段BC的延长线上时,依题意在图2中补全图形并判断(1)中结论是否成立?若成立,请证明;若不成立,请说明理由.
(3)在(1)的条件下,ED与AC相交于点P,若AB=2,直接写出CP的最大值.
分析 (1)先判断出△ABD≌△ACE,进而得出AD=AE,∠BAD=∠CAE,即可判断出△ADE是等腰直角三角形;
(2)直接根据题意画出图形,同(1)的方法即可得出结论;
(3)先判断出PC最大,即可得出AP最小,利用点到直线的距离最小,得出AC⊥DE时,AP最小,最后利用等腰直角三角形的性质即可得出结论.
解答 解:(1)如图1, 连接AE,
连接AE,
∵在Rt△BAC中,∠BAC=90°,AB=AC,
∴∠B=∠ACB=45°.
∵CE⊥BC,
∴∠BCE=90°.
∴∠2=45°.
∴∠B=∠2.
又∵AB=AC,BD=CE,
∴△ABD≌△ACE.
∴AD=AE,∠BAD=∠CAE.
∴∠DAE=∠BAC=90°.
∴△DAE是等腰直角三角形.
∴∠ADE=∠3=45°.
(2)补全图形,如图2所示,
结论成立.
证明:
如图,连接AE,
∵在Rt△BAC中,∠BAC=90°,AB=AC,
∴∠B=∠1=45°.
∵CE⊥BC,
∴∠BCE=90°.
∴∠2=45°.
∴∠B=∠2.
又∵AB=AC,BD=CE,
∴△ABD≌△ACE.
∴AD=AE,∠BAD=∠CAE.
∴∠DAE=∠BAC=90°.
∴△DAE是等腰直角三角形.
∴∠ADE=∠3=45°.
(3)由(1)知,△ADE是等腰直角三角形,
∵AB=2,
∴AC=2,
当AP最小时,CP最大,
即:DE⊥AC时,AP最小,
∵∠ADE=45°,∠ACB=45°,
∴AD⊥BC,AD=$\frac{1}{2}$BC=$\frac{1}{2}$×$\sqrt{2}$AB=$\sqrt{2}$,
在Rt△ADP中,AP=$\frac{\sqrt{2}}{2}$AD=1,
∴CP=AC-AP=1.
即:CP的最大值为1.
点评 此题是三角形综合题,主要考查了全等三角形的判定和性质,等腰直角三角形的判定和性质,极值的确定,解本题的关键是构造全等三角形,判断出△ADE是等腰直角三角形,是一道中等难度的中考常考题.

 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案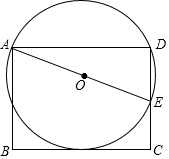 如图,点E为矩形ABCD中CD边上的一点,AB=3,AD=4,以AE为直径的⊙O恰好与BC边相切,则⊙O的半径为$\frac{13}{6}$.
如图,点E为矩形ABCD中CD边上的一点,AB=3,AD=4,以AE为直径的⊙O恰好与BC边相切,则⊙O的半径为$\frac{13}{6}$.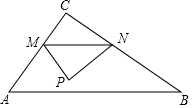 如图,在Rt△ABC中,∠C=90°,AC≠BC,点M是边AC上的动点.过点M作MN∥AB交BC于N,现将△MNC沿MN折叠,得到△MNP.若点P在AB上.则以MN为直径的圆与直线AB的位置关系是相交.
如图,在Rt△ABC中,∠C=90°,AC≠BC,点M是边AC上的动点.过点M作MN∥AB交BC于N,现将△MNC沿MN折叠,得到△MNP.若点P在AB上.则以MN为直径的圆与直线AB的位置关系是相交.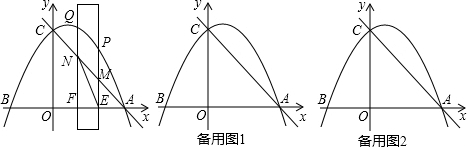
 如图,射线AM平行于射线BN,∠B=90°,AB=4,C是射线BN上的一个动点,连接AC,作CD⊥AC,且AC=2CD,过C作CE⊥BN交AD于点E,设BC长为a.
如图,射线AM平行于射线BN,∠B=90°,AB=4,C是射线BN上的一个动点,连接AC,作CD⊥AC,且AC=2CD,过C作CE⊥BN交AD于点E,设BC长为a.
 将一个正方体如图放置在一个长方体上,则所构成的几何体的左视图可能是( )
将一个正方体如图放置在一个长方体上,则所构成的几何体的左视图可能是( )



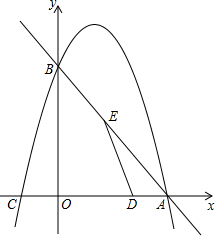 如图,在平面直角坐标系中,直线$y=-\frac{4}{3}x+8$与x轴,y轴分别交于点A、B,抛物线y=ax2-4ax+c经过点A和点B,与x轴的另一个交点为C,动点D从点A出发,以每秒1个单位长度的速度向O点运动,同时动点E从点B出发,以每秒2个单位长度的速度向A点运动,设运动的时间为t秒,0<t<5.
如图,在平面直角坐标系中,直线$y=-\frac{4}{3}x+8$与x轴,y轴分别交于点A、B,抛物线y=ax2-4ax+c经过点A和点B,与x轴的另一个交点为C,动点D从点A出发,以每秒1个单位长度的速度向O点运动,同时动点E从点B出发,以每秒2个单位长度的速度向A点运动,设运动的时间为t秒,0<t<5.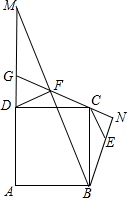 如图,等腰Rt△BNF的直角边FN所在的直线过正方形ABCD的顶点C,且与AD的延长线交于G,BF、AD的延长线交于M,连接DF,CE∥BM交BN于E.
如图,等腰Rt△BNF的直角边FN所在的直线过正方形ABCD的顶点C,且与AD的延长线交于G,BF、AD的延长线交于M,连接DF,CE∥BM交BN于E.